
已知函数f(x)=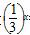 ,x∈[-1,1],函数g(x)=f 2(x)-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=f 2(x)-2af(x)+3的最小值为h(a).
(1)求h(a);
(2)是否存在实数m、n,同时满足以下条件:
①m>n>3;
②当h(a)的定义域为[n,m]时,值域为[n2,m2].
若存在,求出m、n的值;若不存在,说明理由.
科目:高中数学 来源: 题型:
设函数f(x)=ax+bx-cx,其中c>a>0,c>b>0.
(1)记集合M={(a,b,c)|a,b,c不能构成一个三角形的三条边长,且a=b},则(a,b,c)∈M所对应的f(x)的零点的取值集合为________;
(2)若a,b,c是△ABC的三条边长,则下列结论正确的是________.(写出所有正确结论的序号)
①∀x∈(-∞,1),f(x)>0;
②∃x∈R,使ax,bx,cx不能构成一个三角形的三条边长;
③若△ABC为钝角三角形,则∃x∈(1,2),使f(x)=0.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=(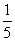 )x-log3x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值( )
)x-log3x,若实数x0是方程f(x)=0的解,且0<x1<x0,则f(x1)的值( )
A.不小于0 B.恒为正数
C.恒为负数 D.不大于0
查看答案和解析>>
科目:高中数学 来源: 题型:
若点(a,b)在y=lgx图像上,a≠1,则下列点也在此图像上的是( )
A.(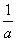 ,b) B.(10a,1-b)
,b) B.(10a,1-b)
C.(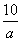 ,b+1) D.(a2,2b)
,b+1) D.(a2,2b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com