
| A. | 8 | B. | 16 | C. | $10\sqrt{3}$ | D. | $8\sqrt{6}$ |
分析 根据平面向量的数量积公式和余弦定理,求出b2+c2=80,再利用基本不等式得出bc的最大值,写出△ABC的面积,求其最大值即可.
解答 解:△ABC中,$\overrightarrow{AB}•\overrightarrow{AC}=|\overrightarrow{AB}-\overrightarrow{AC}|=8$,
设A、B、C所对边分别为a,b,c,
则c•b•cosA=a=8①;
所以△ABC的面积为:
S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$bc$\sqrt{1{-cos}^{2}A}$=$\frac{1}{2}$bc$\sqrt{1-\frac{64}{{{b}^{2}c}^{2}}}$=$\frac{1}{2}$$\sqrt{{{b}^{2}c}^{2}-64}$,
由余弦定理可得b2+c2-2bc•cosA=a2=64②,
由①②消掉cosA得b2+c2=80,
所以b2+c2≥2bc,
bc≤40,当且仅当b=c=2$\sqrt{10}$时取等号,
所以S△ABC=$\frac{1}{2}$$\sqrt{{{b}^{2}c}^{2}-64}$≤$\frac{1}{2}$$\sqrt{{40}^{2}-64}$=8$\sqrt{6}$,
所以△ABC面积的最大值为8$\sqrt{6}$.
故选:D.
点评 本题考查了平面向量数量积的运算、三角形面积公式以及基本不等式的应用问题,是综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱锥P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直线PB上.
在三棱锥P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直线PB上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,M为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,M为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
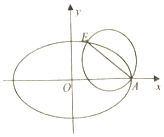 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点为A,离心率为e,且椭圆C过点$E({2e,\frac{b}{2}})$,以AE为直径的圆恰好经过椭圆的右焦点.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右顶点为A,离心率为e,且椭圆C过点$E({2e,\frac{b}{2}})$,以AE为直径的圆恰好经过椭圆的右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{1}{11}$ | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com