Question

17．在直角坐标系xOy中线段AB与y轴垂直，其长度为2，AB的中点C在直线x+2y-4=0上，则tan∠AOB的最大值为$\frac{5\sqrt{3}+8}{11}$．

Answer 1

分析 如图所示．由题意可设A（a，b），B（2+a，b），则线段AB的中点C（a+1，b）．由于AB的中点C在直线x+2y-4=0上，可得a+2b=3．分类讨论：①当a=0时，b=$\frac{3}{2}$．可得tan∠AOB=$\frac{|AB|}{|OA|}$．②当a=-2时，b=$\frac{5}{2}$．可得tan∠AOB=$\frac{|AB|}{|OA|}$．③当b=0时，a=3．可得tan∠AOB=0．④当a≠0，-2且b≠0时，此时k_OA=$\frac{b}{a}$，k_OB=$\frac{b}{2+a}$．当b＞0时，由到角公式得tan∠AOB=$\frac{2}{5b+\frac{15}{b}-16}$．当b＜0时，tan∠AOB=$\frac{2}{16-5b-\frac{15}{b}}$．再利用基本不等式即可得出答案．

解答 解：如图所示．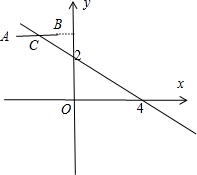
由题意可设A（a，b），B（2+a，b），则线段AB的中点C（a+1，b）．
∵AB的中点C在直线x+2y-4=0上，∴a+1+2b-4=0，化为a+2b=3．
①当a=0时，b=$\frac{3}{2}$．此时A（0，$\frac{3}{2}$），B（2，$\frac{3}{2}$）．
可得tan∠AOB=$\frac{|AB|}{|OA|}$=$\frac{2}{\frac{3}{2}}=\frac{4}{3}$．
②当a=-2时，b=$\frac{5}{2}$．此时A（-2，$\frac{5}{2}$），B（0，$\frac{5}{2}$）．
可得tan∠AOB=$\frac{|AB|}{|OA|}$=$\frac{2}{\frac{5}{2}}=\frac{4}{5}$．
③当b=0时，a=3．此时A（3，0），B（5，0）．
可得tan∠AOB=0．
④当a≠0，-2且b≠0时，此时k_OA=$\frac{b}{a}$，${k}_{OB}=\frac{b}{2+a}$．
当b＞0时，可得tan∠AOB=$\frac{{k}_{OA}-{k}_{OB}}{1+{k}_{OA}•{k}_{OB}}=\frac{\frac{b}{a}-\frac{b}{2+a}}{1+\frac{b}{a}•\frac{b}{2+a}}$=$\frac{2b}{a（2+a）+{b}^{2}}=\frac{2b}{（3-2b）（5-2b）+{b}^{2}}$=$\frac{2}{5b+\frac{15}{b}-16}$．
tan∠AOB≤$\frac{2}{2\sqrt{5b•\frac{15}{b}}-16}$=$\frac{1}{5\sqrt{3}-8}=\frac{5\sqrt{3}+8}{11}$，当且仅当b=$\sqrt{3}$，a=3-2$\sqrt{3}$时取等号．
当b＜0时，tan∠AOB=$\frac{2}{16-5b-\frac{15}{b}}$≤$\frac{1}{8+5\sqrt{3}}$．
综上可知：只有当a=3-2$\sqrt{3}$时，b=$\sqrt{3}$．可得tan∠AOB的最大值为$\frac{5\sqrt{3}+8}{11}$．
故答案为：$\frac{5\sqrt{3}+8}{11}$．

点评 本题考查了直线的斜率计算公式、到角公式、基本不等式，考查了分类讨论和计算能力，属于难题．