
【题目】已知二次函数![]() .
.
(1)画出函数图象并写出顶点坐标和对称轴;

(2)判断奇偶性,并指出单调区间.
(3)求函数![]() 在
在![]() 时的值域.
时的值域.
【答案】(1)图像见解析, 顶点坐标![]() ,对称轴
,对称轴![]() (2)
(2)![]() 是非奇非偶函数函数.
是非奇非偶函数函数.![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减(3)见解析
上单调递减(3)见解析
【解析】
(1)根据函数的解析式作出图象,根据图象直接写出顶点坐标及对称轴即可;(2)由函数图象可得函数的奇偶性以及单调区间;(3)分为![]() ,
,![]() 和
和![]() 三种情形,结合单调性得值域.
三种情形,结合单调性得值域.
解:(1)![]()
![]() ,图象如图所示:
,图象如图所示:
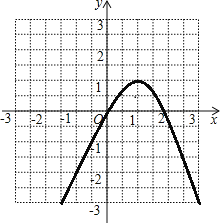
顶点坐标为![]() ,对称轴为
,对称轴为![]() .
.
(2)由图可知:![]() 是非奇非偶函数函数.
是非奇非偶函数函数.
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(3)当![]() 时,
时,![]() 在
在![]() 单调递增,而
单调递增,而![]() ,最大值为
,最大值为![]()
∴![]() 的值域为
的值域为![]() ;
;
当![]() 时,
时,![]() 在
在![]() 单调上递增,在
单调上递增,在![]() 上单调递减,
上单调递减,
而![]() ,最大值为
,最大值为![]() ,
,
∴![]() 的值域为
的值域为![]() ;
;
当![]() 时,
时,![]() 在
在![]() 单调上递增,在
单调上递增,在![]() 上单调递减,
上单调递减,
最小值为![]() ,最大值为
,最大值为![]() ,
,
∴![]() 的值域为
的值域为![]() ,
,
综上可得![]() 的值域为:当
的值域为:当![]() 时,值域为
时,值域为![]() ;当
;当![]() ,值域为
,值域为![]() ;当
;当![]() 时,值域为
时,值域为![]() .
.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,短轴长和焦距都等于2,
轴上,短轴长和焦距都等于2,![]() 是椭圆上的一点,且
是椭圆上的一点,且![]() 在第一象限内,过
在第一象限内,过![]() 且斜率等于
且斜率等于![]() 的直线与椭圆
的直线与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
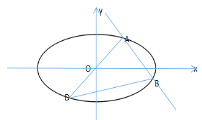
(1)求椭圆![]() 的方程;
的方程;
(2)证明:直线![]() 的斜率为定值;
的斜率为定值;
(3)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2018·江西联考]交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了80辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
| |
数量 | 20 | 10 | 10 | 20 | 15 | 5 |
以这80辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,![]() .某同学家里有一辆该品牌车且车龄刚满三年,记X为该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
.某同学家里有一辆该品牌车且车龄刚满三年,记X为该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损4000元,一辆非事故车盈利8000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只红铃虫的产卵数y和温度x有关,现收集了6组观测数据于下表中,通过散点图可以看出样本点分布在一条指数型函数y=![]() 的图象的周围.
的图象的周围.
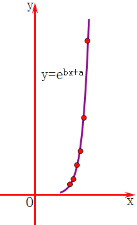
(1)试求出y关于x的上述指数型的回归曲线方程(结果保留两位小数);
(2)试用(1)中的回归曲线方程求相应于点(24,17)的残差![]() .(结果保留两位小数)
.(结果保留两位小数)
温度x(°C) | 20 | 22 | 24 | 26 | 28 | 30 |
产卵数y(个) | 6 | 9 | 17 | 25 | 44 | 88 |
z=lny | 1.79 | 2.20 | 2.83 | 3.22 | 3.78 | 4.48 |
几点说明:
①结果中的![]() 都应按题目要求保留两位小数.但在求
都应按题目要求保留两位小数.但在求![]() 时请将
时请将![]() 的值多保留一位即用保留三位小数的结果代入.
的值多保留一位即用保留三位小数的结果代入.
②计算过程中可能会用到下面的公式:回归直线方程的斜率![]() =
=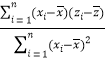 =
=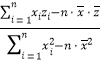 ,截距
,截距![]() .
.
③下面的参考数据可以直接引用:![]() =25,
=25,![]() =31.5,
=31.5,![]() ≈3.05,
≈3.05,![]() =5248,
=5248,![]() ≈476.08,
≈476.08,![]() ,ln18.17≈2.90.
,ln18.17≈2.90.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() .若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是
.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 为左右焦点,
为左右焦点,![]() 为短轴端点,长轴长为4,焦距为
为短轴端点,长轴长为4,焦距为![]() ,且
,且![]() ,
,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程
的方程
(Ⅱ)设动直线![]() 椭圆
椭圆![]() 有且仅有一个公共点
有且仅有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() .试探究:在坐标平面内是否存在定点
.试探究:在坐标平面内是否存在定点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在求出点
?若存在求出点![]() 的坐标,若不存在.请说明理由.
的坐标,若不存在.请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
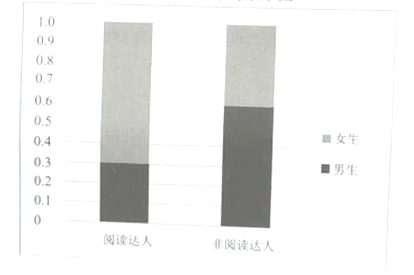
【题目】为了解学生的课外阅读时间情况,某学校随机抽取了 50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:

若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作出如图所示的等高条形图.
(1)根据抽样结果估计该校学生的每天平均阅读时间(同一组数据用该区间的中点值作为代表);
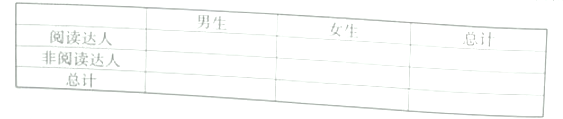
(2)根据已知条件完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“阅读达人”跟性别有关?
的把握认为“阅读达人”跟性别有关?
附:参考公式
![]() ,其中
,其中![]() .
.
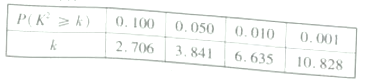
临界值表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设E,F分别是正方体ABCD﹣A1B1C1D1的棱DC上两点,且AB=2,EF=1,给出下列四个命题:
①三棱锥D1﹣B1EF的体积为定值;
②异面直线D1B1与EF所成的角为45°;
③D1B1⊥平面B1EF;
④直线D1B1与平面B1EF所成的角为60°.
其中正确的命题为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com