
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,短轴长和焦距都等于2,
轴上,短轴长和焦距都等于2,![]() 是椭圆上的一点,且
是椭圆上的一点,且![]() 在第一象限内,过
在第一象限内,过![]() 且斜率等于
且斜率等于![]() 的直线与椭圆
的直线与椭圆![]() 交于另一点
交于另一点![]() ,点
,点![]() 关于原点的对称点为
关于原点的对称点为![]() .
.
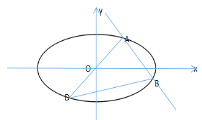
(1)求椭圆![]() 的方程;
的方程;
(2)证明:直线![]() 的斜率为定值;
的斜率为定值;
(3)求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式: 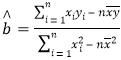 ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下述三个事件按顺序分别对应三个图象,正确的顺序是( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;(2)我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速.
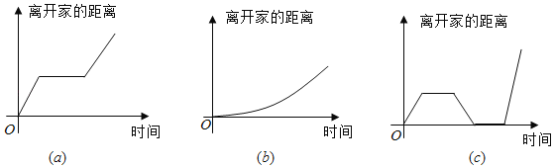
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,左顶点B与右焦点
,左顶点B与右焦点![]() 之间的距离为3.
之间的距离为3.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设直线![]() 交
交![]() 轴于点
轴于点![]() ,过
,过![]() 且斜率不为
且斜率不为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于两点
相交于两点![]() ,连接
,连接![]() 并延长分别与直线
并延长分别与直线![]() 交于两点
交于两点![]() . 若
. 若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(0,+∞)上的函数f(x),对于任意的m,n∈(0,+∞),都有f(mn)=f(m)+f(n)成立,当x>1时,f(x)<0.
(1)求证:1是函数f(x)的零点;
(2)求证:f(x)是(0,+∞)上的减函数;
(3)当f(2)=![]() 时,解不等式f(ax+4)>1.
时,解不等式f(ax+4)>1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com