
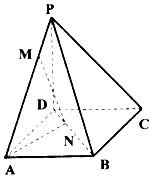
 如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.
如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.分析 (1)延长AN,交CD于点G,由相似知$\frac{AN}{NG}=\frac{BN}{ND}=\frac{AM}{MP}$,推出MN∥PG,然后证明直线MN∥平面PCD;
(2)以DA,DC,DP为x,y,z轴建立空间直角坐标系,设A(1,0,0),求出相关点的坐标,
$\overrightarrow{PB}$=(1,1,-1),平面AMN的法向量,利用向量的数量积求解PB与平面AMN夹角的余弦值.
解答 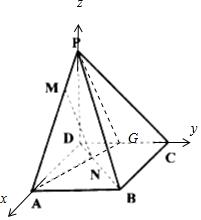 (1)证明:延长AN,交CD于点G,由相似知$\frac{AN}{NG}=\frac{BN}{ND}=\frac{AM}{MP}$,可得:MN∥PG,
(1)证明:延长AN,交CD于点G,由相似知$\frac{AN}{NG}=\frac{BN}{ND}=\frac{AM}{MP}$,可得:MN∥PG,
MN?平面PCD,PG?平面PCD,
则直线MN∥平面PCD;
(2)解:由于DA⊥DC⊥DP,以DA,DC,DP为x,y,z轴建立空间直角坐标系,
设A(1,0,0),则B(1,1,0),C(0,1,0),P(0,0,1),$M(\frac{1}{2},0,\frac{1}{2})$,$N(\frac{1}{2},\frac{1}{2},0)$
则$\overrightarrow{PB}$=(1,1,-1),平面AMN的法向量为$\overrightarrow m=(1,1,1)$,
则向量$\overrightarrow{PB}$与$\overrightarrow m$的夹角为θ,则cosθ=$\frac{1}{3}$,
则PB与平面AMN夹角的余弦值为$\frac{{2\sqrt{2}}}{3}$.
点评 本题考查直线与平面平行的判定定理的应用,直线与平面所成角的求法,考查计算能力以及空间想象能力.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
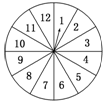 某种日用品上市以后供不应求,为满足更多的消费者,某商场在销售的过程中要求购买这种产品的顾客必须参加如下活动:摇动如下图所示的游戏转盘(上面扇形的圆心角都相等),按照指针所指区域的数字购买商品的件数,每人只能参加一次这个活动.
某种日用品上市以后供不应求,为满足更多的消费者,某商场在销售的过程中要求购买这种产品的顾客必须参加如下活动:摇动如下图所示的游戏转盘(上面扇形的圆心角都相等),按照指针所指区域的数字购买商品的件数,每人只能参加一次这个活动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com