
分析 由关于x的不等式bx2+ax+$\frac{1}{4}$<0有实数解可化为△=a2-b>0;
从而可得关于x的不等式bx2+ax+$\frac{1}{4}$<0有实数解的概率为图中阴影部分与正方形的面积比,得出结果.
解答 解:由题意,若b=0,a≠0时,不等式bx2+ax+$\frac{1}{4}$<0有实数解;
若b≠0,则△=a2-b>0;
作出平面区域如下,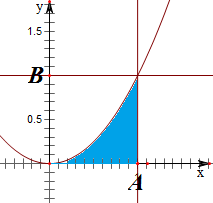
关于x的不等式bx2+ax+$\frac{1}{4}$<0有实数解的概率为图中阴影部分与正方形的面积比,
S阴=${∫}_{0}^{1}$x2dx=$\frac{1}{3}$•x3${|}_{0}^{1}$=$\frac{1}{3}$;
故$\frac{{S}_{阴影}}{{S}_{正方形}}$=$\frac{\frac{1}{3}}{1×1}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了几何概型的概率求法以及作图能力和积分的运算问题,是综合性题目.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
 如图,△ABC内接于⊙O,弦AE交BC于D,已知AD2=BD•DC,∠ADC=60°,OD=1,OE⊥BC.
如图,△ABC内接于⊙O,弦AE交BC于D,已知AD2=BD•DC,∠ADC=60°,OD=1,OE⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1588 | B. | 0.1587 | C. | 0.1586 | D. | 0.1585 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
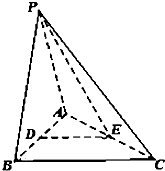 如图,在三棱锥P-ABC中,△PAB是正三角形,在△ABC中,AB⊥BC,且D、E分别为AB、AC的中点.
如图,在三棱锥P-ABC中,△PAB是正三角形,在△ABC中,AB⊥BC,且D、E分别为AB、AC的中点. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0,1} | C. | {0} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2Sn=an+1 | B. | Sn=2an+1 | C. | 2Sn=an-1 | D. | Sn=2an-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com