
分析 (1)由诱导公式和弦化切可得原式=$\frac{-2sinα+cosα}{sinα+cosα}$=$\frac{-2tanα+1}{tanα+1}$,代值计算可得;
(2)变形并弦化切可得原式=$\frac{3si{n}^{2}α+sinαcosα+2co{s}^{2}α}{si{n}^{2}α+co{s}^{2}α}$=$\frac{3ta{n}^{2}α+tanα+2}{ta{n}^{2}α+1}$,代值计算可得.
解答 解:(1)∵tanα=-2,∴$\frac{2sin(α+π)+cos(2π-α)}{cos(α-\frac{π}{2})-sin(\frac{3π}{2}+α)}$
=$\frac{-2sinα+cosα}{sinα+cosα}$=$\frac{-2tanα+1}{tanα+1}$=$\frac{-2×(-2)+1}{-2+1}$=-5;
(2)sin2α+sinαcosα+2=sin2α+sinαcosα+2sin2α+2cos2α
=3sin2α+sinαcosα+2cos2α=$\frac{3si{n}^{2}α+sinαcosα+2co{s}^{2}α}{si{n}^{2}α+co{s}^{2}α}$
=$\frac{3ta{n}^{2}α+tanα+2}{ta{n}^{2}α+1}$=$\frac{3×(-2)^{2}-2+2}{(-2)^{2}+1}$=$\frac{12}{5}$
点评 本题考查同角三角函数基本关系,弦化切是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:选择题
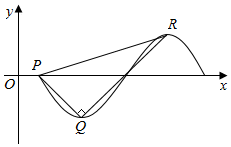 f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是定义在R上的奇函数,如图是该函数在一个周期内的图象.其中P为图象与x轴的交点,Q为最低点,R为最高点,$\overrightarrow{PQ}$•$\overrightarrow{QR}$=0,S△PQR=$\frac{{π}^{2}}{2}$,则方程Asin(ωx+φ)=$\frac{π}{2}$|lgx|的根的个数为( )
f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是定义在R上的奇函数,如图是该函数在一个周期内的图象.其中P为图象与x轴的交点,Q为最低点,R为最高点,$\overrightarrow{PQ}$•$\overrightarrow{QR}$=0,S△PQR=$\frac{{π}^{2}}{2}$,则方程Asin(ωx+φ)=$\frac{π}{2}$|lgx|的根的个数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com