
【题目】如图所示,已知四边形![]() 是菱形,平面
是菱形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() .
.
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由面面垂直的性质定理可得![]() 平面
平面![]() ,再由面面垂直的判定定理得平面
,再由面面垂直的判定定理得平面![]() 平面
平面![]() ;
;
(2)设![]() 与
与![]() 交于点O,连接
交于点O,连接![]() ,可证
,可证![]() 平面
平面![]() .以O为坐标原点,以
.以O为坐标原点,以![]() ,
,![]() ,
,![]() 所在直线分别为x轴、y轴、z轴建立空间直角坐标系
所在直线分别为x轴、y轴、z轴建立空间直角坐标系![]() ,求出平面
,求出平面![]() 和平面
和平面![]() 的法向量,即求二面角
的法向量,即求二面角![]() 的余弦值.
的余弦值.
(1)证明:菱形![]() 中,
中,![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
(2)设![]() 与
与![]() 交于点O,连接
交于点O,连接![]() ,因为
,因为![]() ,且
,且![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() .
.
![]() ,
,![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
以O为坐标原点,以![]() ,
,![]() ,
,![]() 所在直线分别为x轴、y轴、z轴建立空间直角坐标系
所在直线分别为x轴、y轴、z轴建立空间直角坐标系![]() ,如图所示
,如图所示
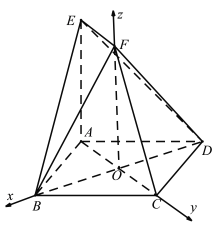
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,即
,即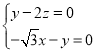 ,令
,令![]() ,则
,则![]() ,
,
![]() .
.
又平面![]() 的法向量为
的法向量为![]() .
.
设二面角![]() 的大小为
的大小为![]() ,则
,则![]() 为锐角.
为锐角.
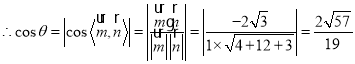 ,
,
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某市教育局为了监控某校高一年级的素质教育过程,从该校高一年级16个班随机抽取了16个样本成绩,制表如下:
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
测评成绩 | 95 | 96 | 96 | 90 | 95 | 98 | 98 | 97 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
测评成绩 | 97 | 95 | 96 | 98 | 99 | 96 | 99 | 96 |
令![]() 为抽取的第
为抽取的第![]() 个学生的素质教育测评成绩,
个学生的素质教育测评成绩,![]() ,经计算得
,经计算得![]() ,
,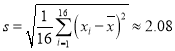 ,
, ,
,![]() ,以下计算精确到0.01.
,以下计算精确到0.01.
(1)求![]() 的相关系数
的相关系数![]() ,并回答
,并回答![]() 与
与![]() 是否可以认为具有较强的相关性;
是否可以认为具有较强的相关性;
(2)在抽取的样本成绩中,如果出现了在![]() 之外的成绩,就认为本学期的素质教育过程可能出现了异常情况,需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议,从该校抽样的结果来看,是否需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议?
之外的成绩,就认为本学期的素质教育过程可能出现了异常情况,需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议,从该校抽样的结果来看,是否需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议?
附:样本![]() 的相关系数
的相关系数 ,若
,若![]() ,则可以认为两个变量具有较强的线性相关性.
,则可以认为两个变量具有较强的线性相关性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴与短轴比值是2,椭圆C过点
的长轴与短轴比值是2,椭圆C过点![]() .
.
(1)求椭圆C的标准方程;
(2)过点![]() 作圆x2+y2=1的切线
作圆x2+y2=1的切线![]() 交椭圆C于A,B两点,记△AOB(O为坐标原点)的面积为S△AOB,将S△AOB表示为m的函数,并求S△AOB的最大值
交椭圆C于A,B两点,记△AOB(O为坐标原点)的面积为S△AOB,将S△AOB表示为m的函数,并求S△AOB的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为圆
为圆![]() 上的动点,过点
上的动点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,动点
,动点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,且满足
,且满足![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天津市某学校组织教师进行“学习强国”知识竞赛,规则为:每位参赛教师都要回答3个问题,且对这三个问题回答正确与否相互之间互不影响,若每答对1个问题,得1分;答错,得0分,最后按照得分多少排出名次,并分一、二、三等奖分别给予奖励.已知对给出的3个问题,教师甲答对的概率分别为![]() ,
,![]() ,p.若教师甲恰好答对3个问题的概率是
,p.若教师甲恰好答对3个问题的概率是![]() ,则
,则![]() ________;在前述条件下,设随机变量X表示教师甲答对题目的个数,则X的数学期望为________.
________;在前述条件下,设随机变量X表示教师甲答对题目的个数,则X的数学期望为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活水平的提高和人们对健康生活的重视,越来越多的人加入到健身运动中.国家统计局数据显示,2019年有4亿国人经常参加体育锻炼.某健身房从参与健身的会员中随机抽取100人,对其每周参与健身的天数和2019年在该健身房所有消费金额(单位:元)进行统计,得到以下统计表及统计图:
平均每周健身天数 | 不大于2 | 3或4 | 不少于5 |
人数(男) | 20 | 35 | 9 |
人数(女) | 10 | 20 | 6 |

若某人平均每周进行健身天数不少于5,则称其为“健身达人”.该健身房规定消费金额不多于1600元的为普通会员,超过1600元但不超过3200元的为银牌会员,超过3200元的为金牌会员.
(1)已知金牌会员都是健身达人,现从健身达人中随机抽取2人,求他们均是金牌会员的概率;
(2)能否在犯错误的概率不超过![]() 的前提下认为性别和是否为“健身达人”有关系?
的前提下认为性别和是否为“健身达人”有关系?
(3)该健身机构在2019年年底针对这100位消费者举办一次消费返利活动,现有以下两种方案:
方案一:按分层抽样从普通会员、银牌会员和金牌会员中共抽取25位“幸运之星”,分别给予188元,288元,888元的幸运奖励;
方案二:每位会员均可参加摸奖游戏,游戏规则如下:摸奖箱中装有5张形状大小完全一样的卡片,其中3张印跑步机图案、2张印动感单车图案,有放回地摸三次卡片,每次只能摸一张,若摸到动感单车的总数为2,则获得100元奖励,若摸到动感单车的总数为3,则获得200元奖励,其他情况不给予奖励.规定每个普通会员只能参加1次摸奖游戏,每个银牌会员可参加2次摸奖游戏,每个金牌会员可参加3次摸奖游戏(每次摸奖结果相互独立).
请你比较该健身房采用哪一种方案时,在此次消费返利活动中的支出较少,并说明理由.
附: ,其中
,其中![]() 为样本容量.
为样本容量.
| 0.50 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| 0.455 | 1.323 | 2.706 | 3.841 | 6.636 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 企业为了监控某种零件的一条流水生产线的产品质量,检验员从该生产线上随机抽取100个零件,测量其尺寸
企业为了监控某种零件的一条流水生产线的产品质量,检验员从该生产线上随机抽取100个零件,测量其尺寸![]() (单位:
(单位:![]() )并经过统计分析,得到这100个零件的平均尺寸为10,标准差为0.5.企业规定:若
)并经过统计分析,得到这100个零件的平均尺寸为10,标准差为0.5.企业规定:若![]() ,该零件为一等品,企业获利20元;若
,该零件为一等品,企业获利20元;若![]() 且
且![]() ,该零件为二等品,企业获利10元;否则,该零件为不合格品,企业损失40元.
,该零件为二等品,企业获利10元;否则,该零件为不合格品,企业损失40元.
(1)在某一时刻内,依次下线10个零件,如果其中出现了不合格品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查若这10个零件的尺寸分别为9.6,10.5,9.8,10.1,10.7,9.4,10.9,9.5,10,10.9,则从这一天抽检的结果看,是否需要对当天的生产过程进行检查?
(2)将样本的估计近似地看作总体的估计通过检验发现,该零件的尺寸![]() 服从正态分布
服从正态分布![]() .其中近似为样本平均数,
.其中近似为样本平均数,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)从下线的零件中随机抽取20件,设其中为合格品的个数为![]() ,求
,求![]() 的数学期望(结果保留整数)
的数学期望(结果保留整数)
(ii)试估计生产10000个零件所获得的利润.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com