
分析 先用圆x2+y2=4上的特殊点C(2,0),D(-2,0),求出满足条件的点A(1,0),B(4,0);
再证明在圆x2+y2=4上任意一点P(x0,y0)到A,B两点的距离之比为常数$\frac{1}{2}$成立即可.
解答 解:假设在x轴正半轴上存在两个定点A(a,0),B(b,0),其中a>0,b>0,
使得圆x2+y2=4上任意一点P(x0,y0)到A,B两点的距离之比为常数$\frac{1}{2}$,
则|PA|=$\frac{1}{2}$|PB|,
不妨取特殊点C(2,0),D(-2,0);
有(2-a)2=$\frac{1}{4}$(2-b)2①,
(-2-a)2=$\frac{1}{4}$(-2-b)2②,
解得a=1,b=4;
所以A(1,0),B(4,0);
现证明在圆x2+y2=4上任意一点P(x0,y0)到A,B两点的距离之比为常数$\frac{1}{2}$,
则${{(x}_{0}-1)}^{2}$+${{y}_{0}}^{2}$=$\frac{1}{4}$[${{(x}_{0}-4)}^{2}$+${{y}_{0}}^{2}$]③,
${{x}_{0}}^{2}$+${{y}_{0}}^{2}$=4④;
把④代入③,并化简得等式恒成立;
所以存在点A(1,0),B(4,0),满足|PA|=$\frac{1}{2}$|PB|成立.
点评 本题考查了直线与圆的方程的应用问题,也考查了转化思想的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题

| A. | 25π | B. | 25$\sqrt{2}$π | C. | 50π | D. | 50$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$$\overrightarrow a$+$\frac{1}{2}$$\overrightarrow b$ | B. | $\frac{1}{2}$$\overrightarrow a$+$\frac{1}{4}$$\overrightarrow b$ | C. | $\frac{2}{3}$$\overrightarrow a$+$\frac{1}{3}$$\overrightarrow b$ | D. | $\frac{1}{2}$$\overrightarrow a$+$\frac{2}{3}$$\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
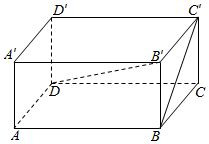 (理科学生做)在长方体ABCD-A′B′C′D′中,AB=4,BC=CC′=2,求
(理科学生做)在长方体ABCD-A′B′C′D′中,AB=4,BC=CC′=2,求查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com