
分析 (1)求出函数的导数,根据f(x)有且只有一个极值点,得到x2-2ax+1<0恒成立,求出a的范围即可;
(2)根据“分界函数”的定义,只需x∈(1,+∞)时,f(x)-(1-a)x2<0恒成立且f(x)-(1-a2)lnx>0恒成立,判断函数的单调性,求出a的范围即可.
解答 解:(1)f′(x)=$\frac{{x}^{2}-2ax+1}{x}$,x∈(1,+∞),
令g(x)=x2-2ax+1,由题意得:g(x)在[1,+∞)有且只有1个零点,
∴g(1)<0,解得:a>1;
(2)若f(x)是函数f1(x)、f2(x)在区间(1,+∞)上的一个“分界函数”,
则x∈(1,+∞)时,f(x)-(1-a)x2<0恒成立且f(x)-(1-a2)lnx>0恒成立,
令h(x)=f(x)-(1-a)x2=(a-$\frac{1}{2}$)x2-2ax+lnx,
则h′(x)=$\frac{[(2a-1)x-1](x-1)}{x}$,
①2a-1≤0即a≤$\frac{1}{2}$时,当x∈(1,+∞)时,h′(x)<0,h(x)递减,且h(1)=-$\frac{1}{2}$-a,
∴h(1)≤0,解得:-$\frac{1}{2}$≤a≤$\frac{1}{2}$;
②2a-1>0即a>$\frac{1}{2}$时,y=(a-$\frac{1}{2}$)x2-2ax的图象开口向上,
存在x0>1,使得(a-$\frac{1}{2}$)${{x}_{0}}^{2}$-2ax0>0,
从而h(x0)>0,h(x)<0在(1,+∞)不恒成立,
令m(x)=f(x)-(1-a2)lnx=$\frac{1}{2}$x2-2ax+a2lnx,
则m′(x)=$\frac{{(x-a)}^{2}}{x}$≥0,m(x)在(1,+∞)递增,
由f(x)-(1-a2)lnx>0恒成立,得:m(1)≥0,解得:a≤$\frac{1}{4}$,
综上,a∈[-$\frac{1}{2}$,$\frac{1}{4}$]时,f(x)是函数f1(x)、f2(x)在区间(1,+∞)上的一个“分界函数”.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及函数恒成立问题,考查新定义问题,是一道综合题.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:选择题
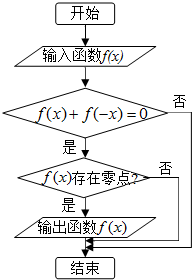
| A. | f(x)=xtanx | B. | f(x)=xex | C. | f(x)=x+2lnx | D. | f(x)=x-sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 2π | C. | 3π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com