
分析 (1)直线l的极坐标方程为:ρsin(θ+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,展开可得:$\frac{\sqrt{2}}{2}$ρ(sinθ+cosθ)=$\frac{\sqrt{2}}{2}$,利用互化公式可得直角坐标方程.曲线C的参数方程为:$\left\{\begin{array}{l}{x=2(sint+cost)}\\{y=4(1+sin2t)}\end{array}\right.(t为参数)$,可得x2=4(1+sin2t)=y,x∈$[-2\sqrt{2},2\sqrt{2}]$.
(2)直线l的参数方程为:$\left\{\begin{array}{l}{x=-1-\frac{\sqrt{2}}{2}t}\\{y=2+\frac{\sqrt{2}}{2}t}\end{array}\right.$,代入曲线C的方程可得:${t}^{2}+\sqrt{2}$t-2=0,可得|AB|=|t1-t2|=$\sqrt{({t}_{1}+t)^{2}-4{t}_{1}{t}_{2}}$,
|PA|•|PB|=|t1t2|.
解答 解:(1)直线l的极坐标方程为:ρsin(θ+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,
展开可得:$\frac{\sqrt{2}}{2}$ρ(sinθ+cosθ)=$\frac{\sqrt{2}}{2}$,可得直角坐标方程:x+y-1=0.
曲线C的参数方程为:$\left\{\begin{array}{l}{x=2(sint+cost)}\\{y=4(1+sin2t)}\end{array}\right.(t为参数)$,x2=4(1+sin2t)=y,x∈$[-2\sqrt{2},2\sqrt{2}]$.
(2)直线l的参数方程为:$\left\{\begin{array}{l}{x=-1-\frac{\sqrt{2}}{2}t}\\{y=2+\frac{\sqrt{2}}{2}t}\end{array}\right.$,代入曲线C的方程可得:${t}^{2}+\sqrt{2}$t-2=0,
∴t1+t2=-$\sqrt{2}$,t1•t2=-2.
∴|AB|=|t1-t2|=$\sqrt{({t}_{1}+t)^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{2+8}$=$\sqrt{10}$,
|PA|•|PB|=|t1t2|=2.
点评 本题考查了极坐标方程化为直角坐标方程的方法、参数方程及其应用、弦长公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
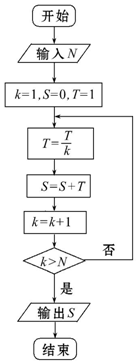
| A. | $1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{10}$ | B. | 1+$\frac{1}{1×2}$+$\frac{1}{1×2×3}$+…+$\frac{1}{1×2×…×10}$ | ||
| C. | $1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{11}$ | D. | 1+$\frac{1}{1×2}$+$\frac{1}{1×2×3}$+…+$\frac{1}{1×2×…×11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若“p∧q”为假命题,则“p∨q”为真命题 | |
| B. | 命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0” | |
| C. | 命题“若x=0,则x2-x=0”的逆否命题为真命题 | |
| D. | 若命题p:?n∈N,n2>2n,则?p:?n∈N,n2≤2n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在△ABC中,角A,B,C的对边分别是a,b,c,则a>b是cos A<cos B的充要条件 | |
| B. | 命题p:对任意的x∈R,x2+x+1>0,则¬p:对任意的x∈R,x2+x+1≤0 | |
| C. | 已知p:$\frac{1}{x+1}$>0,则¬p:$\frac{1}{x+1}$≤0 | |
| D. | 存在实数x∈R,使sin x+cos x=$\frac{π}{2}$成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
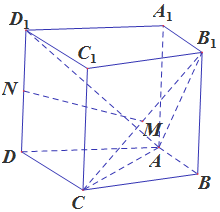 如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果两条直线l1与l2垂直,那么它们的斜率之积一定等于-1 | |
| B. | “a>0,b>0”是“$\frac{b}{a}$+$\frac{a}{b}$≥2”的充分必要条件 | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | “a≠-5或b≠5”是“a+b≠0”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com