已知函数f(x)是(－∞，＋∞)上的增函数，a、b∈R，对命题“若a＋b≥0，则f(a)＋f(b)≥f(－a)＋f(－b)”．
(1)写出其逆命题，判断其真假，并证明你的结论；
(2)写出其逆否命题，判断其真假，并证明你的结论．
解 (1)逆命题是：若f(a)＋f(b)≥f(－a)＋f(－b)，
则a＋b≥0为真命题．
用反证法证明：假设a＋b＜0，则a＜－b，b＜－a.
∵f(x)是(－∞，＋∞)上的增函数，
则f(a)＜f(－b)，f(b)＜f(－a)，
∴f(a)＋f(b)＜f(－a)＋f(－b)，这与题设相矛盾，所以逆命题为真．
(2)逆否命题：若f(a)＋f(b)＜f(－a)＋f(－b)，
则a＋b＜0为真命题．
因为原命题⇔它的逆否命题，所以证明原命题为真命题即可．
∵a＋b≥0, ∴a≥－b，b≥－a.
又∵f(x)在(－∞，＋∞)上是增函数，
∴f(a)≥f(－b)，f(b)≥f(－a)，
∴f(a)＋f(b)≥f(－a)＋f(－b)．
所以逆否命题为真．
阅读快车系列答案科目：高中数学 来源： 题型：
已知圆C1的方程为(x－2)2+(y－1)2=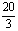
，椭圆C2的方程为
，C2的离心率为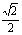
，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径，试求：
（I）直线AB的方程；
（II）椭圆C2的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
已知命题p：∃n∈N,2n＞1 000，则綈p为( )．
A．∀n∈N,2n≤1 000 B．∀n∈N,2n＞1 000
C．∃n∈N,2n≤1 000 D．∃n∈N,2n＜1 000
查看答案和解析>>
科目：高中数学 来源： 题型：
有三个命题：(1)“若x＋y＝0，则x，y互为相反数”的逆命题；
(2)“若a＞b，则a2＞b2”的逆否命题；
(3)“若x≤－3，则x2＋x－6＞0”的否命题．
其中真命题的个数为________(填序号)．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，若
，
，则
的值为 （ ）
B．
C．
D．
a∈(0，＋∞)，
θ∈R，使asinθ≥a成立，则cos(θ－
)的值为 .
则f(f(－2))＝________.