
设f(x)=|lg x|,a,b为实数,且0<a<b.
(1)求方程f(x)=1的解;
(2)若a,b满足f(a)=f(b),求证: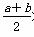 >1.
>1.
(3)在(2)的条件下,求证:由关系式f(b)=2f(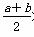 )所得到的关于b的方程g(b)=0,存在b0∈(3,4),使g(b0)=0.
)所得到的关于b的方程g(b)=0,存在b0∈(3,4),使g(b0)=0.
科目:高中数学 来源: 题型:
某汽车厂有一条价值为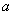 万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值.经过市场调查,产品的增加值
万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值.经过市场调查,产品的增加值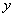 万元与技术改造投入的
万元与技术改造投入的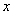 万元之间满足:①
万元之间满足:①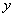 与
与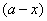 和
和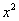 的乘积成正比;②
的乘积成正比;② ,其中
,其中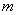 是常数.若
是常数.若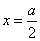 时,
时,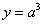 .
.
(1)求产品增加值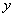 关于
关于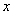 的表达式;(2)求产品增加值
的表达式;(2)求产品增加值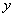 的最大值及相应的
的最大值及相应的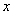 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com