
| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| x | 6 | 8 | 10 | 12 | 14 |
| y | 2 | 3 | 4 | 5 | 6 |
分析 (1)确定基本事件的个数,利用古典概型概率公式,即可求解;
(2)利用公式求出a,b,可得回归直线方程,令x=20,即可得出结论.
解答 解:(1)从这五名学生中任选两名,共有${C}_{5}^{2}$=10种,选出的两名学生的记忆力均超过8有${C}_{3}^{2}$=3种,
∴从这五名学生中任选两名,选出的两名学生的记忆力均超过8的概率为$\frac{3}{10}$;
(2)由题意,$\overline{x}$=10,$\overline{y}$=4,∴b=$\frac{12+24+40+60+84-5×10×4}{36+64+100+144+196-5×100}$=0.5,
a=4-0.5×10=-1,∴y=0.5x-1,
x=20时,y=0.5×20-1=9,
点评 本题考查概率的计算,考查回归直线方程,考查学生的计算能力,正确计算是关键.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 6$\sqrt{2}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b+c,c+a,a+b成等差数列 | B. | $\frac{1}{a}$,$\frac{1}{b}$,$\frac{1}{c}$成等差数列 | ||
| C. | a2-bc,b2-ac,c2-ab成等差数列 | D. | $\frac{1}{\sqrt{a}+\sqrt{b}}$+$\frac{1}{\sqrt{b}+\sqrt{c}}$=$\frac{2}{\sqrt{a}+\sqrt{c}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
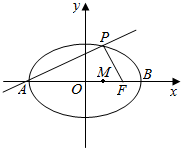 如图所示,点A,B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF,设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|.
如图所示,点A,B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF,设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com