
分析 令 t=cosx∈[-1,1],求得f(x)=g(t)=t-t3,利用导数研究函数g(t)的单调性,从而求得g(t)的最大值.
解答 解:∵函数f(x)=sinx2cosx=cosx(1-cos2x),令 t=cosx∈[-1,1],
则f(x)=g(t)=t-t3,令g′(t)=1-3t2=0,求得t=±$\frac{1}{3}$.
在(-$\frac{1}{3}$,$\frac{1}{3}$)上,g′(t)>0,故g(t)的一个增区间为(-$\frac{1}{3}$,$\frac{1}{3}$);
在[-1,-$\frac{1}{3}$)、($\frac{1}{3}$,1]上,g′(t)<0,故g(t)减区间为[-1,-$\frac{1}{3}$)、($\frac{1}{3}$,1].
再根据g(-1)=0,g($\frac{1}{3}$)=$\frac{8}{27}$,可得g(t)的最大值为g($\frac{1}{3}$)=$\frac{8}{27}$.
点评 本题主要考查同角三角函数的基本关系,利用导数研究函数的单调性,利用单调性求函数的最值,属于中档题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
 如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的C处恰有一可旋转光源满足甲水果生产的需要,该光源照射范围是∠ECF=$\frac{π}{6}$,点E,F的直径AB上,且∠ABC=$\frac{π}{6}$.
如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的C处恰有一可旋转光源满足甲水果生产的需要,该光源照射范围是∠ECF=$\frac{π}{6}$,点E,F的直径AB上,且∠ABC=$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
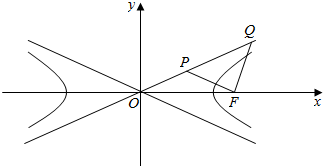
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 甲 | 乙 | 丙 | 丁 | 戊 |
| x | 6 | 8 | 10 | 12 | 14 |
| y | 2 | 3 | 4 | 5 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x∈R,使ex>x2 | B. | ?x0∈R,使ex0<x02 | ||
| C. | ?x0∈R,使ex0≤x02 | D. | ?x∈R,使ex≤x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com