
已知数列{an}中,a1=2,an-an-1-2n=0(n≥2,n∈N*).
(1)写出a2,a3的值(只写结果),并求出数列{an}的通项公式;
(2)设bn=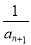 +
+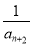 +
+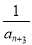 +…+
+…+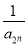 ,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+
,若对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+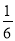 >bn恒成立,求实数t的取值范围.
>bn恒成立,求实数t的取值范围.
(1)a2=6,a3=12. an=n(n+1).
(2)实数t的取值范围为(-∞,-2)∪(2,+∞)
【解析】【解析】
(1)∵a1=2,an-an-1-2n=0(n≥2,n∈N*),
∴a2=6,a3=12.
当n≥3时,an-an-1=2n,an-1-an-2=2(n-1),
又a3-a2=2×3,a2-a1=2×2,
∴an-a1=2[n+(n-1)+…+3+2],
∴an=2[n+(n-1)+…+3+2+1]=2×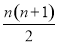 =n(n+1).
=n(n+1).
当n=1时,a1=2;当n=2时,a2=6,也满足上式,
∴数列{an}的通项公式为an=n(n+1).
(2)bn=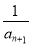 +
+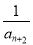 +…+
+…+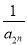
=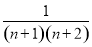 +
+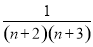 +…+
+…+
=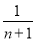 -
-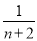 +
+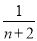 -
-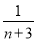 +…+
+…+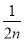 -
-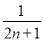
=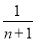 -
-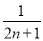
=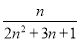
=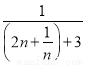 .
.
令f(x)=2x+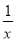 (x≥1),则f′(x)=2-
(x≥1),则f′(x)=2-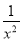 ,
,
当x≥1时,f′(x)>0恒成立,
∴函数f(x)在[1,+∞)上是增函数,
故当x=1时,f(x)min=f(1)=3,
即当n=1时,(bn)max=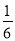 .
.
要使对任意的正整数n,当m∈[-1,1]时,不等式t2-2mt+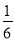 >bn恒成立,则需t2-2mt+
>bn恒成立,则需t2-2mt+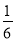 >(bn)max=
>(bn)max=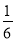 ,
,
即t2-2mt>0对?m∈[-1,1]恒成立,
∴ ,解得t>2或t<-2,
,解得t>2或t<-2,
∴实数t的取值范围为(-∞,-2)∪(2,+∞).


科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-5合情推理与演绎推理(解析版) 题型:选择题
已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是( )
A.(7,5) B.(5,7) C.(2,10) D.(10,1)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-2一元二次不等式及其解法(解析版) 题型:选择题
不等式x2+ax+4<0的解集不是空集,则实数a的取值范围是( )
A.[-4,4] B.(-4,4)
C.(-∞,-4]∪[4,+∞) D.(-∞,-4)∪(4,+∞)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-5数列的综合应用(解析版) 题型:解答题
某企业为加大对新产品的推销力度,决定从今年起每年投入100万元进行广告宣传,以增加新产品的销售收入.已知今年的销售收入为250万元,经市场调查,预测第n年与第n-1年销售收入an与an-1(单位:万元)满足关系式:an=an-1+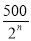 -100.
-100.
(1)设今年为第1年,求第n年的销售收入an;
(2)依上述预测,该企业前几年的销售收入总和Sn最大.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-5数列的综合应用(解析版) 题型:选择题
数列{an}是公差不为0的等差数列,a1=1且a1、a3、a6成等比数列,则{an}的前n项和Sn等于( )
A.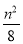 +
+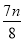 B.
B.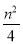 +
+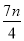
C.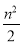 +
+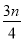 D.n2+n
D.n2+n
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:解答题
已知各项均不相等的等差数列{an}的前n项和为Sn,若S3=15,且a3+1为a1+1和a7+1的等比中项.
(1)求数列{an}的通项公式与前n项和Sn;
(2)设Tn为数列{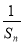 }的前n项和,问是否存在常数m,使Tn=m[
}的前n项和,问是否存在常数m,使Tn=m[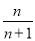 +
+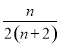 ],若存在,求m的值;若不存在,说明理由.
],若存在,求m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-4数列求和(解析版) 题型:选择题
数列1,1+2,1+2+4,…,1+2+22+…+2n-1,…的前n项和Sn>1020,那么n的最小值是( )
A.7 B.8 C.9 D.10
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-2等差数列及其前n项和(解析版) 题型:填空题
已知数列{an}中a1=1,a2=2,当整数n>1时,Sn+1+Sn-1=2(Sn+S1)都成立,则S15=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:4-4数系的扩充与复数的引入(解析版) 题型:选择题
已知复数z满足(1+i)z=3+i(i为虚数单位),则复数z在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com