
在平面直角坐标系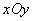 中,已知抛物线
中,已知抛物线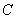 :
: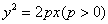 ,在此抛物线上一点
,在此抛物线上一点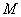
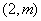 到焦点的距离是3.
到焦点的距离是3.
(1)求此抛物线的方程;
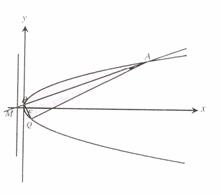
(2)抛物线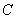 的准线与
的准线与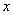 轴交于
轴交于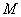 点,过
点,过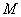 点斜率为
点斜率为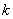 的直线
的直线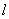 与抛物线
与抛物线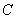 交于
交于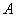 、
、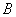 两点.是否存在这样的
两点.是否存在这样的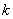 ,使得抛物线
,使得抛物线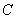 上总存在点
上总存在点 满足
满足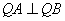 ,若存在,求
,若存在,求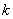 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
科目:高中数学 来源: 题型:
在直角坐标系中,定义两点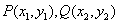 之间的“直角距离”为
之间的“直角距离”为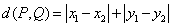
现有下列四个命题:
①已知两点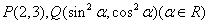 ,则
,则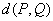 为定值;
为定值;
②原点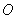 到直线
到直线 上任一点P的直角距离
上任一点P的直角距离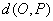 的最小值为
的最小值为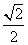 ;与
;与
③若 表示
表示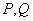 两点间的距离,那么
两点间的距离,那么 ;
;
④设点 且
且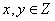 ,若点
,若点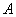 在过点
在过点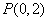 与
与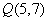 的直线上,且点
的直线上,且点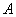 到点
到点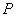 与
与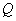 的“直角距离”之和等于10,那么满足条件的点A只有5个。
的“直角距离”之和等于10,那么满足条件的点A只有5个。
其中的真命题是 (写出所有真命题的序号)。
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,已知某探照灯反光镜的纵切面是抛物线的一部分,光源安装在焦点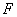 上,且灯的深度
上,且灯的深度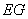 等于灯口直径
等于灯口直径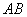 ,且为64
,且为64 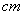 ,则光源安装的位置
,则光源安装的位置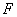 到灯的顶端
到灯的顶端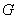 的距离为____________
的距离为____________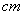 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
观察两相关变量得如下数据:
| x | -9 | -6.99 | -5.01 | -3 |
| y | -9 | -7 | -5 | -3 |
| -5 | 5 | 4 | 4 |
| -4.01 | -4.99 | 5.01 | 3.99 |
则这两变量间的回归直线方程为( )
A.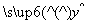 =
=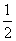 x+1 B.
x+1 B.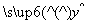 =x C.
=x C.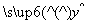 =2x+
=2x+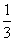 D.
D.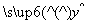 =x+1
=x+1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直二面角α-l-β,点A∈α,AC⊥l,C为垂足,B∈β,BD⊥l,D为垂足,若AB=2,AC=BD=1,
则CD=( )
A. 1 B. 2 C. 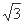 D.
D. 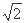
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com