练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．将4名学生分别安排甲、乙、丙三个地方参加实践活动，每个地方至少安排一名学生，则不同的安排方案共有（　　）
    A．12B．18C．24D．36

    分析 根据混合元素的排列问题，把其中的某几个元素组合成一个元素，再进行全排列，问题得以解决

    解答 解：先从4名学生种选择两名组成一个复合元素，然后再将3个元素（包含复合元素）安排到甲、乙，丙三地，不同的安排方案共有C42A33=36种．
    故选：D．

    点评 本题主要考查了排列组合的中混合元素排列问题，关键组合成一个新复合元素，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

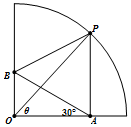    12．现有四分之一圆形的纸板（如图），∠AOB=90°，圆半径为1，要裁剪成四边形OAPB，且满足AP∥OB，∠OAB=30°，∠POA=θ，记此四边形OAPB的面积为f（θ），求f（θ）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．方程（$\frac{1}{3}$）x-x=0的解有（　　）
    A．0个B．3个C．2个D．1个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．为了考察某种药物治疗效果，进行动物试验，得到如下数据：
    患病未患病总计
    服用药10b50
    未服药cd50
    总计3070100
    （1）求出表格中b，c，d的值；
    （2）是否有95%的把握认为该药物有效．
    附：
    i：${k^2}=\frac{{n{{（ad-bc）}^2}}}{{（{a+b}）（{a+d}）（{b+c}）（{b+d}）}}$
    ii：
    P（k2≥k）0.150.050.0250.005
    k2.0723.8415.0247.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．若函数f（x）=loga（8-ax）满足：对任意x1，x2∈（0，2]（x1≠x2），都有（x1-x2）[f（x1）-f（x2）]＜0，则实数a的取值范围是（　　）
    A．（0，1）B．（1，4）C．（1，4]D．（4，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．f（x）=x2-2x+alnx．
    （Ⅰ）若a=2，求f（x）在点（1，f（1））处的切线方程；
    （Ⅱ）讨论f（x）的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．某射击手射击一次命中的概率为0.8，连续两次均射中的概率是0.5，已知某次射中，则随后一次射中的概率是（　　）
    A．$\frac{5}{8}$B．$\frac{3}{8}$C．$\frac{4}{5}$D．$\frac{2}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知数列{an}中，已知${a_1}=\frac{2}{3}$，a2=1，2an=3an-1-an-2（n≥3）．
    （1）求a3的值；
    （2）证明：数列{an-an-1}（n≥2）是等比数列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

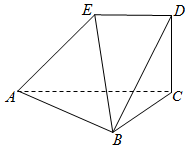    12．如图，AC=2ED，AC∥平面EDB，AC⊥平面BCD，平面ACDE⊥平面ABC．
    （Ⅰ）求证：AC∥ED；
    （Ⅱ）求证：DC⊥BC；
    （Ⅲ）当BC=CD=DE=1时，求二面角A-BE-D的余弦值；
    （Ⅳ）在棱AB上是否存在点P满足EP∥平面BDC；
    （Ⅴ）设$\frac{CD}{CE}$=k，是否存在k满足平面ABE⊥平面CBE？若存在求出k值，若不存在说明理由．

    查看答案和解析>>

    同步练习册答案