
分析 a1=1,an+1=2Sn+3,n=1时,a2=2a1+3=5.n≥2时,an=2Sn-1+3,相减可得:an+1-an=2an,即an+1=3an,
数列{an}从第二项开始为等比数列.利用通项公式即可得出.
解答 解:∵a1=1,an+1=2Sn+3,
∴n=1时,a2=2a1+3=5.
n≥2时,an=2Sn-1+3,相减可得:an+1-an=2an,即an+1=3an,
∴数列{an}从第二项开始为等比数列.
an=5×3n-2.
∴an=$\left\{\begin{array}{l}{1,n=1}\\{5×{3}^{n-2},n≥2}\end{array}\right.$.(n∈N*).
故答案为:$\left\{\begin{array}{l}{1,n=1}\\{5×{3}^{n-2},n≥2}\end{array}\right.$.(n∈N*).
点评 本题考查了数列递推关系、等比数列的通项公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | y平均减少2.5个单位 | B. | y平均减少0.5个单位 | ||
| C. | y平均增加2.5个单位 | D. | y平均增加0.5个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 30 | C. | 45 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
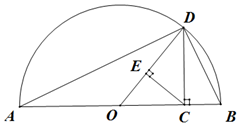 若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )| A. | $CD,CE,\frac{2ab}{a+b}≥\sqrt{ab}$ | B. | $CD,DE,\frac{2ab}{a+b}≤\sqrt{ab}$ | C. | $CD,CE,\frac{2ab}{a+b}≥\sqrt{ab}$ | D. | $CD,CE,\frac{2ab}{a+b}≤\sqrt{ab}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=9,则x=±3”的否命题为“若x2=9,则x≠±3” | |
| B. | 若命题P:?x0∈R,$x_0^2-3{x_0}-1>0$,则命题?P:?x∈R,$x_{\;}^2-3x-1<0$ | |
| C. | 设$\overrightarrow a,\overrightarrow b$是两个非零向量,则“$\overrightarrow a•\overrightarrow b<0$是“$\overrightarrow a,\overrightarrow b$夹角为钝角”的必要不充分条件 | |
| D. | 若命题P:$\frac{1}{x-2}>0$,则¬P:$\frac{1}{x-2}≤0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com