
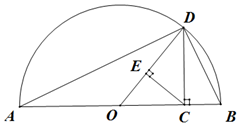
 ��a��0��b��0�����$\frac{2ab}{a+b}$Ϊa��b�ĵ���ƽ��������ͼ����CΪ�߶�AB�ϵĵ㣬��AC=a��BC=b����OΪ�߶�AB�е㣬��ABΪֱ������Բ������C��AB�Ĵ��߽���Բ��D������OD��AD��BD������C��OD�Ĵ��ߣ�����ΪE����ͼ���߶�OD�ij�����a��b������ƽ��������ôͼ�б�ʾa��b�ļ���ƽ���������ƽ�������߶Σ��Լ��ɴ˵õ��IJ��ȹ�ϵ�ֱ��ǣ�������
��a��0��b��0�����$\frac{2ab}{a+b}$Ϊa��b�ĵ���ƽ��������ͼ����CΪ�߶�AB�ϵĵ㣬��AC=a��BC=b����OΪ�߶�AB�е㣬��ABΪֱ������Բ������C��AB�Ĵ��߽���Բ��D������OD��AD��BD������C��OD�Ĵ��ߣ�����ΪE����ͼ���߶�OD�ij�����a��b������ƽ��������ôͼ�б�ʾa��b�ļ���ƽ���������ƽ�������߶Σ��Լ��ɴ˵õ��IJ��ȹ�ϵ�ֱ��ǣ�������| A�� | $CD��CE��\frac{2ab}{a+b}��\sqrt{ab}$ | B�� | $CD��DE��\frac{2ab}{a+b}��\sqrt{ab}$ | C�� | $CD��CE��\frac{2ab}{a+b}��\sqrt{ab}$ | D�� | $CD��CE��\frac{2ab}{a+b}��\sqrt{ab}$ |
���� �������������μ���ͼ����߶εij������ö���ó����߶ε����壬����ֱ�DZ�С��б�ߵó���С��ϵ��
��� �⣺��Rt��ACD�ס�RtDCB�ã�$\frac{AC}{CD}=\frac{CD}{CB}$����$\frac{a}{CD}=\frac{CD}{b}$��
��CD=$\sqrt{ab}$�����߶�CD��ʾa��b�ļ���ƽ������
��OC=AC-OA=a-$\frac{a+b}{2}$=$\frac{a-b}{2}$��
��sin��OCE=sin��ODC=$\frac{OC}{OD}$=$\frac{\frac{a-b}{2}}{\frac{a+b}{2}}$=$\frac{a-b}{a+b}$��
��OE=OC•sin��OCE=$\frac{��a-b��^{2}}{2��a+b��}$��
��DE=OD-OE=$\frac{a+b}{2}$-$\frac{��a-b��^{2}}{2��a+b��}$=$\frac{2ab}{a+b}$�����߶�DE��ʾa��b�ĵ���ƽ������
��a��bʱ���������ε����ʿ�֪DE��CD����$\frac{2ab}{a+b}$��$\sqrt{ab}$��
��a=bʱ��OD��CD�غϣ���ʱE��O��C�����غϣ���DE=CD����$\frac{2ab}{a+b}=\sqrt{ab}$��
��ѡB��
���� ���⿼����Բ�����ʣ�ƽ�����ļ������壬�����е��⣮


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | $\frac{8}{3}$ | B�� | $\frac{4}{3}$ | C�� | $\frac{{8\sqrt{2}}}{3}$ | D�� | $\frac{{4\sqrt{2}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 5 �� | C�� | 4�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| P��K2��k0�� | 0.10 | 0.05 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
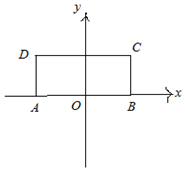 ��ͼ���ھ���ABCD�У�AB=12��BC=5����A��BΪ�����˫����$M��\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ǡ�ù�C��D���㣬��˫����M�ı�����Ϊ$\frac{x^2}{16}-\frac{y^2}{20}=1$��
��ͼ���ھ���ABCD�У�AB=12��BC=5����A��BΪ�����˫����$M��\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ǡ�ù�C��D���㣬��˫����M�ı�����Ϊ$\frac{x^2}{16}-\frac{y^2}{20}=1$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com