
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
分析 (Ⅰ)由表中的数据分别计算,即可写出线性回归方程;
(Ⅱ)由线性回归方程,计算x=10时,的值即可.
解答 解:(1)由表中的数据得$\overline{x}$=30000,$\overline{y}$=5,$\sum_{i=1}^{5}$xiyi=627000,$\sum_{i=1}^{5}$${{x}_{i}}^{2}$=5500000000
∴b=$\frac{627000-5×30000×5}{5500000000-5×900000000}$≈-0.000123
∴a=5-0.000123×30000=1.31,
∴所求线性回归方程为y=-0.000123x+1.31;
(2)由(1)得,z=x(y-2)=x(-0.000123x-0.69),无解.
点评 本题考查了求线性回归方程的应用问题,也考查了利用线性回归方程预测生产问题,是基础题目.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:选择题
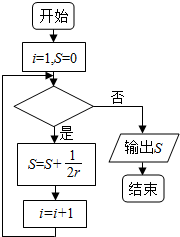
| A. | i≤1006 | B. | i≤1007 | C. | i>1007 | D. | i>1006 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,抛物线y2=4x的焦点为F,动点T(-1,m),过F作TF的垂线交抛物线于P,Q两点,弦PQ的中点为N.
如图所示,抛物线y2=4x的焦点为F,动点T(-1,m),过F作TF的垂线交抛物线于P,Q两点,弦PQ的中点为N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com