
【题目】已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx
(1)当a=1时,求f(x)的单调区间;
(2)若函数f(x)在(0, ![]() )上无零点,求a最小值.
)上无零点,求a最小值.
【答案】
(1)解:当a=1时,f(x)=x﹣1﹣2lnx,
则f′(x)=1﹣ ![]() ,由f′(x)>0,得x>2,
,由f′(x)>0,得x>2,
由f′(x)<0,得0<x<2,
故f(x)的单调减区间为(0,2],单调增区间为[2,+∞).
(2)解:因为f(x)<0在区间(0, ![]() )上恒成立不可能,
)上恒成立不可能,
故要使函数f(x)在(0, ![]() )上无零点,只要对任意的x∈(0,
)上无零点,只要对任意的x∈(0, ![]() ),f(x)>0恒成立,
),f(x)>0恒成立,
即对x∈(0, ![]() ),a>2﹣
),a>2﹣ ![]() 恒成立.
恒成立.
令l(x)=2﹣ ![]() ,x∈(0,
,x∈(0, ![]() ),
),
则l′(x)= ![]() ,
,
再令m(x)=2lnx+ ![]() ﹣2,x∈(0,
﹣2,x∈(0, ![]() ),
),
则m′(x)=﹣ ![]() +
+ ![]() =
= ![]() <0,
<0,
故m(x)在(0, ![]() )上为减函数,于是m(x)>m(
)上为减函数,于是m(x)>m( ![]() )=2﹣2ln2>0,
)=2﹣2ln2>0,
从而l(x)>0,于是l(x)在(0, ![]() )上为增函数,
)上为增函数,
所以l(x)<l( ![]() )=2﹣4ln2,
)=2﹣4ln2,
故要使a>2﹣ ![]() 恒成立,只要a∈[2﹣4ln2,+∞),
恒成立,只要a∈[2﹣4ln2,+∞),
综上,若函数f(x)在(0, ![]() )上无零点,则a的最小值为2﹣4ln2.
)上无零点,则a的最小值为2﹣4ln2.
【解析】(1)先求出函数f(x)的导数,再令f′(x)>0得单调增区间,令f′(x)<0得单调减区间;(2)先将已知转化为恒成立问题,再利用导数可得函数的单调性,进而可得a的取值范围,从而可得a的最小值.


科目:高中数学 来源: 题型:
【题目】设数列![]() 的通项公式为
的通项公式为![]() (
(![]() ,
, ![]() ),数列
),数列![]() 定义如下:对于正整数
定义如下:对于正整数![]() ,
, ![]() 是使得不等式
是使得不等式![]() 成立的所有
成立的所有![]() 中的最小值.
中的最小值.
(1)若![]() ,
, ![]() ,求
,求![]() ;
;
(2)若![]() ,
, ![]() ,求数列
,求数列![]() 的前
的前![]() 项和公式;
项和公式;
(3)是否存在![]() 和
和![]() ,使得
,使得![]()
![]() ?如果存在,求
?如果存在,求![]() 和
和![]() 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为 ![]() +
+ ![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线 ![]() ﹣
﹣ ![]() =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 ![]() .
.
(1)求椭圆C的方程;
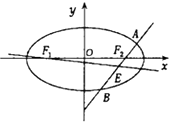
(2)设F1 , F2分别为椭圆C的左,右焦点,过F2作直线l(与x轴不重合)交于椭圆于A,B两点,线段AB的中点为E,记直线F1E的斜率为k,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1.
(1)求证:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a>0且a≠1,函数f(x)=![]() x2-(a+1)x+alnx.
x2-(a+1)x+alnx.
(1)当a=2时,求曲线y=f(x)在(3,f(3))处切线的斜率;
(2)求函数f(x)的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,在下列命题中,其中正确命题的序号是.
,在下列命题中,其中正确命题的序号是.
⑴曲线 ![]() 必存在一条与
必存在一条与 ![]() 轴平行的切线;
轴平行的切线;
⑵函数 ![]() 有且仅有一个极大值,没有极小值;
有且仅有一个极大值,没有极小值;
⑶若方程 ![]() 有两个不同的实根,则
有两个不同的实根,则 ![]() 的取值范围是
的取值范围是 ![]() ;
;
⑷对任意的 ![]() ,不等式
,不等式 ![]() 恒成立;
恒成立;
⑸若 ![]() ,则
,则 ![]() ,可以使不等式
,可以使不等式 ![]() 的解集恰为
的解集恰为 ![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有六间不同的电脑室,每天晚上至少开放两间,欲求不同安排方案的种数,现有3位同学分别给出了下列三个结果:① ![]() ;②26-7;③
;②26-7;③ ![]() ,其中正确的结论是( )
,其中正确的结论是( )
A.仅有①
B.仅有②
C.②与③
D.仅有③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com