
| A. | 命题“负数的平方是正数”不是全称命题 | |
| B. | 命题“?x∈N,x3>x”的否定是“?x∈N,x3>x” | |
| C. | “a=1”是“函数f(x)=sin 2ax的最小正周期为π”的必要不充分条件 | |
| D. | “b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
分析 A,命题“负数的平方是正数”的含义为“任意一个负数的平方都是正数”,是全称命题,可判断A;
B,写出命题“?x∈N,x3>x”的否定,可判断B;
C,利用充分必要条件的概念,从充分性与必要性两个方面可判断C;
D,利用充分必要条件的概念与偶函数的定义可判断D.
解答 解:对于A,命题“负数的平方是正数”是全称命题,故A错误;
对于B,命题“?x∈N,x3>x”的否定是“?x∈N,x3≤x”,故B错误;
对于C,a=1时,函数f(x)=sin 2ax=sin2x,其最小正周期为T=$\frac{2π}{2}$=π,充分性成立;
反之,若函数f(x)=sin2ax的最小正周期T=$\frac{2π}{|a|}$=π,则a=±1,必要性不成立;
∴“a=1”是函数f(x)=sin2ax的最小正周期为π的充分不必要条件,故C错误;
对于D,b=0时,函数f(x)=ax2+c,f(-x)=a(-x)2+c=ax2+c=f(x),y=f(x)是偶函数,充分性成立;
反之,若函数f(x)=ax2+bx+c是偶函数,则f(-x)=f(x),即ax2-bx+c=ax2+bx+c,得bx=0恒成立,即b=0,必要性成立.
∴“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件,故D正确.
故选:D
点评 本题考查命题的真假判断与应用,着重考查全称命题与特称命题之间的转化及充分必要条件的概念及应用,考查函数的周期性与奇偶性,属于中档题.


科目:高中数学 来源: 题型:解答题
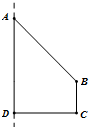 如图,在四边形ABCD中,AD⊥DC,AD∥BC,AD=3,CD=2,$AB=2\sqrt{2}$,∠DAB=45°,四边形绕着直线AD旋转一周,
如图,在四边形ABCD中,AD⊥DC,AD∥BC,AD=3,CD=2,$AB=2\sqrt{2}$,∠DAB=45°,四边形绕着直线AD旋转一周,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x(元) | 14 | 16 | 18 | 20 | 22 |
| Y(件) | 12 | 10 | 7 | 53 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | 3 | C. | -3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com