（本题12分）
已知函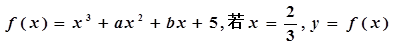
有极值，且曲线
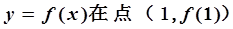处的切线斜率为3.
（1）求函数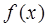
的解析式；
（2）求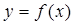
在[－4，1]上的最大值和最小值。
（3）函数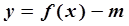
有三个零点，求实数
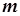的取值范围.
（1）
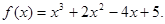
（2）
上的最大值为13，最小值为－11。
（3）
。
解析试题分析：（1）利用导数的几何意义得到参数a,b的值。
科目：高中数学
来源：
题型：解答题
（本小题满分12分）设
科目：高中数学
来源：
题型：解答题
已知函数
科目：高中数学
来源：
题型：解答题
（12分）已知函数
科目：高中数学
来源：
题型：解答题
（本小题满分14分）
科目：高中数学
来源：
题型：解答题
（本小题满分14分）已知函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
（2）求解导数判定函数的单调性，进而得到极值，和端点值，比较大小得到最值。
（3）根据函数单调性，确定极大值和极小值的符号，使得有三个零点。
解：（1）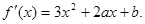
……………………1分
由题意，得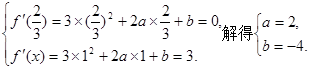
…………3分
所以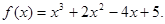， …………………………4分
（2）由（1）知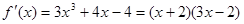
令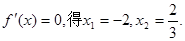
……………………5分x －4 （－4，
－2）－2 （－2， 
）（ ，1）1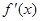 
+ 0 － 0 +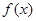 
↗ 极大值 ↘ 极小值 ↗ 函数值 －-11 
练习册系列答案
填充图册中国地图出版社系列答案
第1考卷课时卷系列答案
书立方吉林专版系列答案
奇迹课堂系列答案
初中伴你学习新课程系列答案
同步训练与闯关系列答案
新支点卓越课堂系列答案
优干线测试卷系列答案
优干线课课练系列答案
相关习题
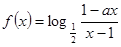为奇函数，a为常数。
（1）求a的值；
（2）证明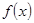
在区间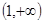
上为增函数；
（3）若对于区间
上的每一个
的值，不等式
恒成立，求实数m 的取值范围。
．
（1）讨论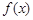
的单调性；
（2）设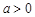
，证明：当
时，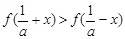
；
（3）若函数
的图像与x轴交于A，B两点，线段AB中点的横坐标为x0，证明：
（x0）＜0．（本题满分14分）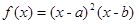
（
）.
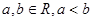①当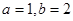
时，求曲线
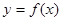在点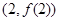
处的切线方程；
②设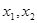
是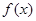
的两个极值点，
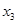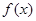是的一个零点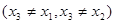
.证明：存在实数
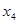，使得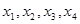
按某种顺序排列后构成等差数列，并求.
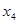已知函数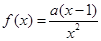
，其中
.
（Ⅰ）求函数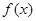
的单调区间；
（Ⅱ）若直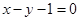线
是曲线
的切线，求实数
的值；
（Ⅲ）设
，求
在区间
上的最大值.（其中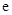
为自然对数的底数）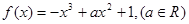
（1）若在
的图象上横坐标为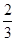
的点处存在垂直于y 轴的切线，求a 的值；
（2）若在区间（-2，3）内有两个不同的极值点，求a 取值范围；
（3）在（1）的条件下，是否存在实数m，使得函数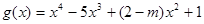
的图象与函数的图象恰有三个交点，若存在，试出实数m 的值；若不存在，说明理由．
同步练习册答案
版权声明：本站所有文章，图片来源于网络，著作权及版权归原作者所有，转载无意侵犯版权，如有侵权，请作者速来函告知，我们将尽快处理，联系qq：3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号
时，不等式
恒成立，求实数k的取值范围；
.
．
时，求曲线
在点
处的切线方程；
时，讨论
的单调性.
在点
的切线方程为
.
的解析式；
，求证：
在
上恒成立.