
分析 画出球的内接直三棱ABC-A1B1C1,作出球的半径,然后可求球的表面积.
解答 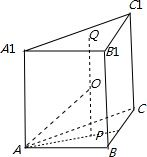 解:直三棱ABC-A1B1C1的各顶点都在同一球面上,
解:直三棱ABC-A1B1C1的各顶点都在同一球面上,
若AB=3,AC=2,∠BAC=60°,
则BC=$\sqrt{9+4-2×3×2×\frac{1}{2}}$=$\sqrt{7}$,
如图,连接上下底面外心,O为PQ的中点,OP⊥平面ABC,
则球的半径为OA,
由题意,AP=$\frac{1}{2}×\frac{\sqrt{7}}{\frac{\sqrt{3}}{2}}$=$\sqrt{\frac{7}{3}}$,OP=$\frac{\sqrt{6}}{3}$,
∴OA=$\sqrt{\frac{7}{3}+\frac{6}{9}}$=$\sqrt{3}$,
所以球的表面积为:4πR2=12π.
故答案为:12π.
点评 本题考查球的体积和表面积,球的内接体问题,考查学生空间想象能力理解失误能力,是中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:选择题
| A. | $y={(\frac{1}{2})^{|x|}}$ | B. | y=x2+2|x| | C. | y=|lnx| | D. | y=2-x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=b<c | B. | a=b>c | C. | a<b<c | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
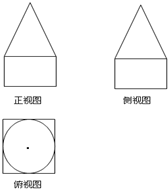 如图,是一个几何体的三视图,正视图和侧视图都是由一个边长为2的等边三角形和一个长为2宽为1的矩形组成.
如图,是一个几何体的三视图,正视图和侧视图都是由一个边长为2的等边三角形和一个长为2宽为1的矩形组成.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{15}$+$\frac{{y}^{2}}{10}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{15}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com