
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上一点,且
上一点,且![]() ,
,![]() .
.
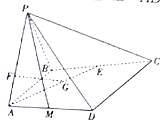
(1)确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)试问:直线![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ,若存在,求
,若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】如下图,已知椭圆![]() 的上顶点为
的上顶点为![]() ,左、右顶点为
,左、右顶点为![]() ,右焦点为
,右焦点为![]() ,
, ![]() ,且
,且![]() 的周长为14.
的周长为14.
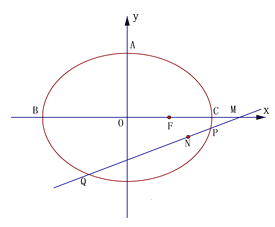
(I)求椭圆的离心率;
(II)过点![]() 的直线
的直线![]() 与椭圆相交于不同两点
与椭圆相交于不同两点![]() ,点N在线段
,点N在线段![]() 上.设
上.设![]() ,试判断点
,试判断点![]() 是否在一条定直线上,并求实数λ的取值范围.
是否在一条定直线上,并求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】编号为A,B,C,D,E的5个小球放在如图所示的5个盒子里,要求每个盒子只能放1个小球,且A球不能放在1,2号盒子里,B球必须放在与A球相邻的盒子中,求不同的放法有多少种?
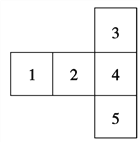
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某校新、老校区之间开车单程所需时间为![]() ,
, ![]() 只与道路畅通状况有关,对其容量为
只与道路畅通状况有关,对其容量为![]() 的样本进行统计,结果如图:
的样本进行统计,结果如图:
| 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,我海监船在![]() 岛海域例行维权巡航,某时刻航行至
岛海域例行维权巡航,某时刻航行至![]() 处,此时测得其东北方向与它相距
处,此时测得其东北方向与它相距![]() 海里的
海里的![]() 处有一外国船只,且
处有一外国船只,且![]() 岛位于海监船正东
岛位于海监船正东![]() 海里处.
海里处.
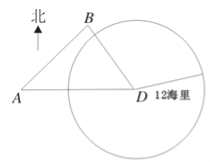
(1)求此时该外国船只与![]() 岛的距离;
岛的距离;
(2)观测中发现,此外国船只正以每小时![]() 海里的速度沿正南方向航行,为了将该船拦截在离
海里的速度沿正南方向航行,为了将该船拦截在离![]() 岛
岛![]() 海里处,不让其进入
海里处,不让其进入![]() 岛
岛![]() 海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:
海里内的海域,试确定海监船的航向,并求其速度的最小值.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与
两点,与![]() 轴,
轴, ![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() ,且
,且![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,
轴的对称点, ![]() 的延长线交椭圆于点
的延长线交椭圆于点![]() ,过点
,过点![]() 分别做
分别做![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
(1) 若椭圆![]() 的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点
的左、右焦点与其短轴的一个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上,求椭圆
上,求椭圆![]() 的方程;
的方程;
(2)当![]() 时,若点
时,若点![]() 平分线段
平分线段![]() ,求椭圆
,求椭圆![]() 的离心率.
的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:
分公司名称 | 雅雨 | 雅鱼 | 雅女 | 雅竹 | 雅茶 |
月销售额 | 3 | 5 | 6 | 7 | 9 |
月利润额 | 2 | 3 | 3 | 4 | 5 |
在统计中发现月销售额![]() 和月利润额
和月利润额![]() 具有线性相关关系.
具有线性相关关系.
(1)根据如下的参考公式与参考数据,求月利润额![]() 与月销售额
与月销售额![]() 之间的线性回归方程;
之间的线性回归方程;
(2)若该总公司还有一个分公司“雅果”月销售额为10万元,试估计它的月利润额是多少?
(参考公式: 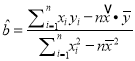 ,
, ![]() ,其中:
,其中: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地最近十年粮食需求量逐年上升,下表是部分统计数据:
年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量与年份之间的回归方程![]() =
=![]() x+
x+![]() ;
;
(2)利用(1)中所求出的直线方程预测该地2018年的粮食需求量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com