已知函数
.
（1）当
时，求函数
的单调递增区间；
（2）设
的内角
的对应边分别为
，且
若向量
与向量
共线，求
的值.
（1）
；(2) 
解析试题分析：（1）因为函数所以通过二倍角公式及三角函数的化一公式，将函数
化简，再通过正弦函数的单调递增区间公式，将化简得到变量
代入相应的x的位置即可求出函数的单调递增区间，从而调整k的值即可得到结论.
(2)由（1）可得函数的解析式，再由
即可求得角C的值.在根据向量共线即可求得一个等式，再根据正弦定理以及余弦定理，即可求得相应的结论.
试题解析：(I)
=
=
令
，
解得
即
,f(x)的递增区间为
(2)由
,得
而
,所以
,所以
得
因为向量与向量共线，所以
，
由正弦定理得:
①
由余弦定理得:
,即a2+b2－ab=9 ②
由①②解得
考点：1.二倍角公式.2.化一公式.3.三角函数的单调性.4.解三角形.
科目：高中数学 来源： 题型：解答题
函数f(x)＝Asin 
＋1(A＞0，ω＞0)的最大值为3，其图象相邻两条对称轴之间的距离为
.
(1)求函数f(x)的解析式；
(2)设α∈
，f
＝2，求α的值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
设函数f(x)=msinx+cosx(x∈R)的图象经过点(
,1).
(1)求f(x)的解析式,并求函数的最小正周期.
(2)若f(α+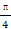
)=
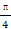且α∈(0,),求f(2α-)的值.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知a>0,函数f(x)=-2asin(2x+
)+2a+b,当x∈[0,
]时,-5≤f(x)≤1.
(1)求常数a,b的值.
(2)设g(x)=f(x+)且lg g(x)>0,求g(x)的单调区间.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
的周期为
.
（1）若
，求它的振幅、初相；
（2）在给定的平面直角坐标系中作出该函数在
的图像；
（3）当时，根据实数
的不同取值，讨论函数
的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
).
． 的部分图象如图所示，其中点
是图象的一个最高点.
的解析式；
且
，求
．
；
是第三象限角，且
，求
，cos(α＋β)＝－
，求cos(α－β)的值．