考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由椭圆方程结合椭圆的离心率求得m的值,再由
=(x
1,
),
=(x
2,
)且
•=0得到
x1x2+=0,首先分析直线AB的斜率存在时,设出直线方程,和椭圆方程联立,利用根与系数关系得到A,B两点横纵坐标的乘积,代入
x1x2+=0得到直线AB的斜率和截距的关系,然后写出△AOB的面积,最后结果不能把变量消掉,说明△AOB的面积不是定值.
解答:
解:由椭圆
+=1(m>4),得b=2,
∵e=
=
,
∴
==1-=,则a
2=16,即m=16.
∴椭圆的方程为
+=1.
向量
=(x
1,
),
=(x
2,
),
由
,的夹角为
,得
•=0,即
x1x2+=0,
当直线AB斜率存在时,设直线AB方程为:y=kx+m,
联立
,消去y得(1+4k
2)x
2+8kmx+4m
2-16=0,
∴△=64k
2m
2-4(1+4k
2)(4m
2-16)>0,
x1+x2=-,
x1x2=,
∴4x
1x
2+y
1y
2=4x
1x
2+(kx
1+m)(kx
2+m)
=(4+k
2)x
1x
2+km(x
1+x
2)+m
2=0,
即(4+k
2)•
-
+m
2=0,
化简得17m
2-16k
2-64=0,
S△AOB=|-
||y
1-y
2|
=
|m||x
1-x
2|
=
|m|
=
|m|
=16|m|
•.不是定值.
点评:本题考查了椭圆的简单几何性质,考查了平面向量在解题中的应用,考查了计算能力,是压轴题.



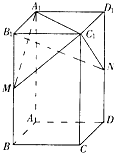 如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.