
分析 (Ⅰ)由题意,抛物线x2=2py上点P处的切线方程为x-y-1=0,设P的坐标,求函数的导函数在P点斜率为1,求解P的坐标值.
(Ⅱ)由题意,采用设而不求的思想,设A(x1,y1)和B(x2,y2)为抛物线上的两个动点,已知y1+y2=4,线段AB的垂直平分线l与y轴交于点C,可以利用中点坐标公式.求解出直线方程,与抛物线组成方程组,求其中点坐标范围.利用弦长公式求|AB|的长度,再求C点到直线AB的距离最大值,从而求解△ABC面积的最大值.
解答 解:(Ⅰ)设点$P({x_0},\frac{x_0^2}{2p})$,由x2=2py得$y=\frac{x^2}{2p}$,求导$y\;'=\frac{x}{p}$,
抛物线x2=2py上点P处的切线方程为x-y-1=0,
∴直线PQ的斜率为1,所以$\frac{x_0}{p}=1$且${x_0}-\frac{{{x_0}^2}}{2p}-1=0$,
解得p=2,
所以:抛物线的方程为x2=4y.
(Ⅱ)设线段AB中点M(x0,y0),则${x_0}=\frac{{{x_1}+{x_2}}}{2},{y_0}=\frac{{{y_1}+{y_2}}}{2}$,${k_{AB}}=\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}=\frac{{\frac{{{x_2}^2}}{4}-\frac{{{x_1}^2}}{4}}}{{{x_2}-{x_1}}}=\frac{1}{4}({{x_1}+{x_2}})=\frac{x_0}{2}$,
∴直线l的方程为$y-2=-\frac{2}{x_0}(x-{x_0})$,
即2x+x0(-4+y)=0,∴l过定点(0,4).即C的坐标为(0,4).
联立$\left\{\begin{array}{l}AB:y-2=\frac{x_0}{2}(x-{x_0})\\{x^2}=4y\end{array}\right.⇒{x^2}-2x{x_0}+2x_0^2-8=0$
得$△=4x_0^2-4(2x_0^2-8)>0⇒-2\sqrt{2}<{x_0}<2\sqrt{2}$,|AB|=$\sqrt{1+\frac{{{x_0}^2}}{4}}|{{x_1}-{x_2}}|$=$\sqrt{(1+\frac{{{x_0}^2}}{4})({32-4x_0^2})}=\sqrt{(4+{x_0}^2)({8-x_0^2})}$,
设C(0,4)到AB的距离$d=|{CM}|=\sqrt{x_0^2+4}$,∴${S_{△ABC}}=\frac{1}{2}|{AB}|•d=\frac{1}{2}\sqrt{(4+{x_0}^2{)^2}({8-x_0^2})}$=$\frac{1}{2}\sqrt{\frac{1}{2}({x_0}^2+4)({x_0^2+4})(16-2x_0^2)}≤\frac{1}{2}\sqrt{\frac{1}{2}{{(\frac{24}{3})}^3}}=8$.
当且仅当$x_0^2+4=16-2x_0^2$,即x0=±2时取等号,
∴S△ABC的最大值为8.
点评 本题考查了导数的几何意义,直线与抛物线相交问题,弦长问题、“点差法”、点到直线的距离公式、三角形的面积计算公式,考查了推理能力与计算能力,属于难题.


 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
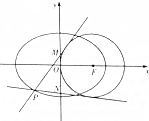 已知离心率为$\frac{{\sqrt{2}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F是圆(x-1)2+y2=1的圆心,过椭圆上的动点P作圆两条切线分别交y轴于M,N(与P点不重合)两点.
已知离心率为$\frac{{\sqrt{2}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F是圆(x-1)2+y2=1的圆心,过椭圆上的动点P作圆两条切线分别交y轴于M,N(与P点不重合)两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a⊥α,α∥β,b?β⇒a⊥b | B. | α∥β,a∥b,a⊥α⇒b⊥β | C. | a∥b,b⊥β⇒a⊥β | D. | a∥b,a∥α⇒b∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢户外运动 | 不喜欢户外运动 | 合计 | |
| 男性 | 5 | ||
| 女性 | 10 | ||
| 合计 | 50 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com