
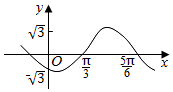
分析 根据图象求出A,ω 和φ,即可求函数f(x)的解析式;
解答 解:由图象的最高点可知,A=$\sqrt{3}$,三角函数的周期:$\frac{5π}{6}-\frac{π}{3}=\frac{1}{2}T$,解得:T=π,那么:$ω=\frac{2π}{T}=\frac{2π}{π}=2$.
当x=$\frac{π}{3}$时,函数值y=0,即$\sqrt{3}$cos(2$•\frac{π}{3}$+φ)=$\sqrt{3}$cos($\frac{π}{2}$+2kπ)
解得:2$•\frac{π}{3}$+φ=2kπ$-\frac{π}{2}$(k∈Z)
∵|φ|<π,∴φ=$\frac{5π}{6}$.
所以解析式 y=$\sqrt{3}$$cos(2x+\frac{5π}{6})$.
故答案为y=$\sqrt{3}$$cos(2x+\frac{5π}{6})$.
点评 本题主要考查三角函数的图象和性质,根据图象求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | c>a>b | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3>b3 | B. | |a|<|b| | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{10}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com