
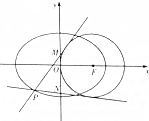
 已知离心率为$\frac{{\sqrt{2}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F是圆(x-1)2+y2=1的圆心,过椭圆上的动点P作圆两条切线分别交y轴于M,N(与P点不重合)两点.
已知离心率为$\frac{{\sqrt{2}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F是圆(x-1)2+y2=1的圆心,过椭圆上的动点P作圆两条切线分别交y轴于M,N(与P点不重合)两点.分析 (1)根据圆方程可求得圆心坐标,即椭圆的右焦点,根据椭圆的离心率进而求得a,最后根据a,b和c的关系求得b,则椭圆方程可得;
(2)P(x0,y0),M(0,m),N(0,n),把椭圆方程与圆方程联立求得交点的横坐标,进而可推断x0的范围,把直线PM的方程化简,根据点到直线的距离公式表示出圆心到直线PM和PN的距离.求得x0和y0的关系式,进而求得m+n和mn的表达式,进而求得|MN|.把点P代入椭圆方程根据弦长公式求得MN|.记f(x)=2-$\frac{4}{(x-2)^{2}}$,根据函数的导函数判断函数的单调性,进而确定函数f(x)的值域,进而求得当x0=-$\sqrt{2}$,时,|MN|取得最大值,进而求得y0,则P点坐标可得.
解答 解:由圆(x-1)2+y2=1的圆心坐标为:(1,0),
∴c=1,
由e=$\frac{c}{a}$=$\frac{{\sqrt{2}}}{2}$,即a=$\sqrt{2}$,
∴b2=a2-c2=1,
∴椭圆方程$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)设P(x0,y0),M(0,m),N(0,n),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{(x-1)^{2}+{y}^{2}=1}\end{array}\right.$,解得:x=2-$\sqrt{2}$,x=2+$\sqrt{2}$(舍去),
∴x0=(-$\sqrt{2}$,0)∪(0,2-$\sqrt{2}$),
直线PM的方程为:y-m=$\frac{{y}_{0}-m}{{x}_{0}}$x,即(y0-m)x-x0y+mx0=0,
∴$\frac{丨{y}_{0}-m+{x}_{0}m丨}{\sqrt{({y}_{0}-m)^{2}+{x}_{0}^{2}}}$=1,
∴(x0-2)m2+2y0m-x0=0,
同理可知:(x0-2)n2+2y0n-x0=0,
∴m和n是方程:(x0-2)t2+2y0t-x0=0的两个根,
∴m+n=-$\frac{2{y}_{0}}{{x}_{0}-2}$,mn=$\frac{-{x}_{0}}{{x}_{0}-2}$,
∴丨MN丨=丨m-n丨=$\sqrt{(m+n)^{2}-4mn}$=$\sqrt{\frac{4{x}_{0}^{2}+4{y}_{0}^{2}-8{x}_{0}}{({x}_{0}-2)^{2}}}$,
∴$\frac{{x}_{0}^{2}}{2}+{y}_{0}^{2}=1$,
∴丨MN丨=$\sqrt{2-\frac{4}{({x}_{0}-2)^{2}}}$,
记f(x)=2-$\frac{4}{(x-2)^{2}}$,则f′(x)=$\frac{8}{(x-2)^{3}}$,
∴x∈(-$\sqrt{2}$,0)时,f'(x)<0;x∈(0,2-$\sqrt{2}$)时,f'(x)<0,
∴f(x)在(-$\sqrt{2}$,0)上单调递减,在(0,2-$\sqrt{2}$)内也是单调递减,
显然,由f(x)的单调性可知:f(x)max=2$\sqrt{\sqrt{2}-1}$,
∴丨MN丨max=2$\sqrt{\sqrt{2}-1}$,
此时x0=-$\sqrt{2}$,
故P点坐标为(-$\sqrt{2}$,0),为椭圆左顶点.
点评 本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查了椭圆的标准方程、简单几何性质、一元二次方程根与系数的关系和利用导数研究函数的单调性等知识,属于中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-8=0 | B. | 2x-y-8=0 | C. | 2x+y+8=0 | D. | 2x-y+8=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com