下列命题中是真命题的是( )
A．若向量a，b满足a·b＝0，则a＝0或b＝0
B．若a<b，则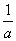
>
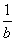
C．若b2＝ac，则a，b，c成等比数列
D．∃x∈R，使得sinx＋cosx＝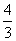
成立
名校课堂系列答案科目：高中数学 来源： 题型：
已知集合A＝{(x，y)|x、y为实数，且x2＋y2＝1}，B＝{(x，y)|x、y为实数，且y＝－x＋1}，则A∩B的元素个数为________．
查看答案和解析>>
科目：高中数学 来源： 题型：
下列四个命题中的真命题为( )
A．∃x0∈Z,1<4x0<3 B．∃x0∈Z,5x0＋1＝0
C．∀x∈R，x2－1＝0 D．∀x∈R，x2＋x＋2>0
查看答案和解析>>
科目：高中数学 来源： 题型：
下列有关命题的说法正确的是( )
A．命题“若x2＝1，则x＝1”的否命题为：“若x2＝1，则x≠1”
B．“x＝－1”是“x2－5x－6＝0”的必要不充分条件
C．命题“∃x∈R，使得x2＋x＋1<0”的否定是：“∀x∈R，均有x2＋x＋1<0”
D．命题“若x＝y，则cosx＝cosy”的逆否命题为真命题
查看答案和解析>>
科目：高中数学 来源： 题型：
在平面直角坐标系xOy中，直线l与抛物线y2＝2x相交于A、B两点．
(1)求证：“如果直线l过点T(3,0)，那么
＝3”是真命题；
(2)写出(1)中命题的逆命题，判断它是真命题还是假命题，并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
给出下列命题：
(1)若q≤1，则方程x2＋2x＋q＝0有实根；
(2)若x、y都是奇数，则x＋y是偶数；
(3)若x＝1或x＝2，则x2－3x＋2＝0；
(4)已知a、b、c是空间三条不同的直线，若a⊥b，且a⊥c，则b∥c.
其否命题为真命题的序号是________．(写出所有符合题意的序号)
查看答案和解析>>
科目：高中数学 来源： 题型：
设x、y是两个实数，命题“x、y中至少有一个数大于1”成立的充分不必要条件是( )
A．x＋y＝2 B．x＋y>2
C．x2＋y2>2 D．xy>1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
则f(2014)等于( )