
分析 (1)运用离心率公式和渐近线方程求得交点M,由两点的距离公式可得a=2,c=4,求得b,进而得到双曲线的方程;
(2)由M,F1的坐标可得直线为y=$\frac{\sqrt{3}}{5}$(x+4),代入双曲线的方程,求得交点A,再由三角形的面积公式计算即可得到所求值.
解答 解:(1)由题意可得e=$\frac{c}{a}$=2,
将直线x=$\frac{{a}^{2}}{c}$,代入渐近线方程y=$\frac{b}{a}$x,可得交点M($\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),
由题意可得|MO|=$\sqrt{\frac{{a}^{4}}{{c}^{2}}+\frac{{a}^{2}{b}^{2}}{{c}^{2}}}$=2,由c2=a2+b2,可得a=2,c=4,
b=$\sqrt{{c}^{2}-{a}^{2}}$=2$\sqrt{3}$,
即有双曲线的方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1;
(2)经过点M(1,$\sqrt{3}$),F1(-4,0)的直线为y=$\frac{\sqrt{3}}{5}$(x+4),
代入双曲线的方程3x2-y2=12,
可得6x2-2x-29=0,
解得x=$\frac{1-5\sqrt{7}}{6}$(舍去)或x=$\frac{1+5\sqrt{7}}{6}$,
即有A($\frac{1+5\sqrt{7}}{6}$,$\frac{5\sqrt{3}+\sqrt{21}}{6}$),
可得△AF1F2面积为$\frac{1}{2}$•8•$\frac{5\sqrt{3}+\sqrt{21}}{6}$=$\frac{10\sqrt{3}+2\sqrt{21}}{3}$.
点评 本题考查双曲线的方程的求法,注意运用离心率公式和渐近线方程,考查三角形的面积的求法,注意运用直线方程和双曲线方程联立,求交点,考查运算能力,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3] | B. | (-∞,1] | C. | [1,2] | D. | [-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
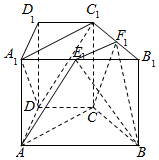 如图,在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为直角梯形,其中AB∥CD,AB⊥AD,AB=AC=2CD=2,AA1=$\sqrt{3}$,过AC的平面分别与A1B1,B1C1交于E1,F1,且E1为A1B1的中点.
如图,在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为直角梯形,其中AB∥CD,AB⊥AD,AB=AC=2CD=2,AA1=$\sqrt{3}$,过AC的平面分别与A1B1,B1C1交于E1,F1,且E1为A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | $(-∞,\frac{1}{2}]∪(1,2]$ | C. | (0,2] | D. | $(0,\frac{1}{2}]∪(1,2]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
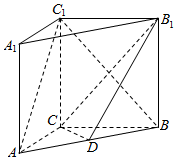 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 车流量(万辆) | 0~10 | 11~50 | 51~70 | 71~80 | 81~100 | >100 |
| 拥挤等级 | 优 | 良 | 轻度拥挤 | 中度拥挤 | 重度拥挤 | 严重拥挤 |
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 107日 |
| 车流量(万辆) | 120 | 110 | 85 | 75 | 60 | 105 | 110 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,0) | B. | (-$\frac{1}{3}$,1) | C. | (0,2) | D. | (-$\frac{1}{3}$,log32) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com