
���� ��I���ɴӸ����꼶��18��ѧ���������ȡ����ũ��ͳ��е�ѧ����10�����������ǵ��������ݣ���������Ҷͼ���Ӷ��õ����еĸ���ѧ����ƽ�����߱�ũ��ĸ���ѧ����ƽ�����ߣ�
��II������ũ������߲�����170�ĸ���ѧ����5�ˣ���5�������ߵ���175����2�ˣ��ɴ����õȿ����¼����ʼ��㹫ʽ���������ǡ������ͬѧ�����ߵ���175�ĸ��ʣ�
��� ����С������12�֣�
�⣺��I���ɴӸ����꼶��18��ѧ���������ȡ����ũ��ͳ��е�ѧ����10�����������ǵ��������ݣ�
������Ҷͼ������ͼ��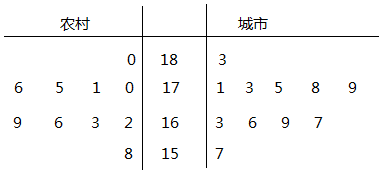
���ۣ����еĸ���ѧ����ƽ�����߱�ũ��ĸ���ѧ����ƽ�����ߣ�
��II������ũ������߲�����170�ĸ���ѧ����5�ˣ�
��5�������ߵ���175����2�ˣ�
����5�������ȡ3��ͬѧ����n=C${\;}_{5}^{3}$=10 ��
���������ǡ������ͬѧ�����ߵ���175����m=${C}_{2}^{2}{C}_{3}^{1}$=3�֣�
������ǡ������ͬѧ�����ߵ���175�ĸ���Ϊp=$\frac{m}{n}$=$\frac{3}{10}$��
���� ���⿼�龥Ҷͼ��������������ʵ����������ݴ���������������������Լ�Ӧ����ʶ�������Ȼ���Ȼ˼��ȣ��ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=0 | B�� | x=1��y=0 | C�� | x=2��y=0 | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com