
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为t元(t为常数,且2≤t≤5),设该食品厂每公斤蘑菇的出厂价为x元(25≤x≤40),根据市场调查,日销售量q与ex成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100kg.(每日利润=日销售量×(每公斤出厂价-成本价-加工费)).
(1)求该工厂的每日利润y元与每公斤蘑菇的出厂价x元的函数关系式;
(2)若t=5,当每公斤蘑菇的出厂价x为多少元时,该工厂的利润y最大,并求最大值.
科目:高中数学 来源: 题型:
甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动,在本次海选中有合格和不合格两个等级.若海选合格记1分,海选不合格记0分.假设甲、乙、丙海选合格的概率分别为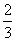 ,
,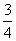 ,
,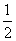 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的.
(1)求在这次海选中,这三名音乐爱好者至少有一名海选合格的概率;
(2)记在这次海选中,甲、乙、丙三名音乐爱好者所得分之和为随机变量ξ,求随机变量ξ的分布列和数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知一组样本点(xi,yi),(其中i=1,2,3,…,30),变量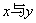 线性相关,且根据最小二乘法求得的回归方程是
线性相关,且根据最小二乘法求得的回归方程是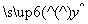 =
=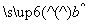 x+
x+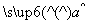 ,则下列说法正确的是 ( )
,则下列说法正确的是 ( )
A.至少有一个样本点落在回归直线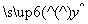 =
=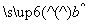 x+
x+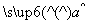 上
上
B.若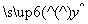 =
=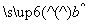 x+
x+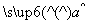 斜率
斜率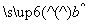 >0,则变量x与y正相关
>0,则变量x与y正相关
C.对所有的解释变量xi (i=1,2,3,…,30),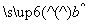 xi+
xi+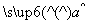 的值与yi有误差
的值与yi有误差
D.若所有样本点都在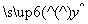 =
=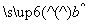 x+
x+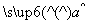 上,则变量间的相关系数为1
上,则变量间的相关系数为1
查看答案和解析>>
科目:高中数学 来源: 题型:
通过随机询问110名大学生是否爱好某项运动,得到如下的列联表
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
由上表算得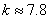 ,因此得到的正确结论是
,因此得到的正确结论是
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C. 有99%以上的把握认为“爱好该项运动与性别有关”
D. 有99%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com