
分析 (I)利用数列递推关系与等比数列的通项公式可得an.利用等差数列的通项公式与求和公式即可得出bn.
(II)利用裂项求和方法、数列的单调性即可得出.
解答 解:(Ⅰ)由3an=2Sn+3,当n=1时,3a1=2a1+3,解得a1=3;
当n≥2时,3an-1=2Sn-1+3,
从而3an-3an-1=2an,即an=3an-1,∴数列{an}是等比数列,公比为3,
因此an=3n.
设数列{bn}的公差为d,∵T5=25,b10=19.
∴$\left\{\begin{array}{l}{5{b}_{1}+10d=25}\\{{b}_{1}+9d=19}\end{array}\right.$,解得b1=1,d=2,
因此bn=2n-1.
(Ⅱ)由(Ⅰ)可得:cn=$\frac{{a}_{n}{b}_{n}}{n(n+1)}$=$\frac{(2n-1)•{3}^{n}}{n(n+1)}$=$\frac{[3n-(n+1)]•{3}^{n}}{n(n+1)}$=$\frac{{3}^{n+1}}{n+1}$-$\frac{{3}^{n}}{n}$,
数列{cn}的前n项和Rn=$(-\frac{3}{1}+\frac{{3}^{2}}{2})$+$(-\frac{{3}^{2}}{2}+\frac{{3}^{3}}{3})$+…+$(-\frac{{3}^{n}}{n}+\frac{{3}^{n+1}}{n+1})$
=$\frac{{3}^{n+1}}{n+1}$-3.
因为cn>0,所以数列{Rn}单调递增.
所以n=1时,Rn取最小值时,故最小值为$\frac{3}{2}$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、裂项求和方法、数列的单调性、数列递推关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源:2016-2017学年河北省高二理上第一次月考数学试卷(解析版) 题型:选择题
在直角坐标系中,已知A(-1,2),B(3,0),那么线段AB中点的坐标为( ).
A.(2,2)
B.(1,1)
C.(-2,-2)
D.(-1,-1)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图时,若输入a,b分别为18,27,则输出的a=( )
下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图时,若输入a,b分别为18,27,则输出的a=( )| A. | 0 | B. | 9 | C. | 18 | D. | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若a>1,则a2>1”的否命题为:“若a>1,则a2≤1” | |
| B. | 命题“?x0>1,使得-x02+2x0-1≥0”的否定“?x≤1,使得-x2+2x-1<0” | |
| C. | “x>-1”是“$\frac{1}{x}<-1$”成立的必要不充分条件 | |
| D. | 正弦函数是奇函数,f(x)=sin(x2+1)是正弦函数,所以f(x)=sin(x2+1)是奇函数,上述推理错误的原因是大前提不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
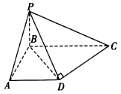 如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA与CD所成角等于60°.
如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA与CD所成角等于60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{11}{3}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com