
分析 求出函数的周期,利用f($\frac{2}{3}$)=1,求解f($\frac{1000}{3}$)即可.
解答 解:f(x+1)+f(1-x)=0 得f(x+1)=-f(1-x) 则f(x)=f(x-1+1)=-f[1-(x-1)]=-f(2-x) 又由f(x+2)-f(2-x)=0 得f(2-x)=f(x+2)则f(x)=-f(x+2)则T=4.f($\frac{2}{3}$)=1,
则f($\frac{1000}{3}$)=f(333+$\frac{1}{3}$)=f(1+$\frac{1}{3}$)=-f(1-$\frac{1}{3}$)=-f($\frac{2}{3}$)=-1.
故答案为:-1.
点评 本题考查抽象函数的应用,函数值的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
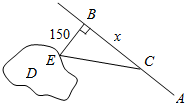 如图,一海岛D,海岛离岸边最近点B的距离是150km,在岸边距点B300km的点A处有一批物资需运往海岛D,为了尽快送达海岛,A与B之间有一铁路,现用海陆联运的方式,火车的时速为50km,船的时速为30km,试在岸边选一点C,问选在何处可使运输时间最短.
如图,一海岛D,海岛离岸边最近点B的距离是150km,在岸边距点B300km的点A处有一批物资需运往海岛D,为了尽快送达海岛,A与B之间有一铁路,现用海陆联运的方式,火车的时速为50km,船的时速为30km,试在岸边选一点C,问选在何处可使运输时间最短.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | i≤2011 | B. | i>2011 | C. | i≤1005 | D. | i>1005 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{4}$ | B. | π | C. | $\frac{{\sqrt{3}π}}{3}$ | D. | $\frac{{2\sqrt{3}}}{9}{π^2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com