
【题目】设数列![]() 是等差数列,数列
是等差数列,数列![]() 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
【答案】(1)an=2n﹣1,bn=3n.(2)当n=1时,Tn=2anbn;当n≥2时,Tn<2anbn.
【解析】
(1)用等差数列和等比数列的基本量法求解;
(2)用错位相减法求和.然后用作差法比较大小.
(1)设等差数列{an}公差为d,等比数列{bn}公比为q.
∵a1=1,b1=3,a2+b3=30,a3+b2=14,
∴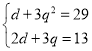 ,化为2q2﹣q﹣15=0,q=3(
,化为2q2﹣q﹣15=0,q=3(![]() 舍去).
舍去).
∴q=3,d=2.
∴an=1+2(n﹣1)=2n﹣1,bn=3n.
(2)cn=(an+1)bn=2n3n,
∴Tn=2(3+2×32+…+n3n),
3Tn=2[32+2×33+…+(n﹣1)×3n+n3n+1],
∴﹣2Tn=2(3+32+…+3n﹣n×3n+1)=2 (1﹣2n)×3n+1﹣3,
(1﹣2n)×3n+1﹣3,
∴Tn![]() .
.
又2anbn=2(2n﹣1)×3n.
∴Tn﹣2anbn![]() 2(2n﹣1)×3n
2(2n﹣1)×3n![]() ,
,
当n=1时,Tn=2anbn,
当n≥2时,Tn<2anbn.


科目:高中数学 来源: 题型:
【题目】如图,已知直线![]() :
:![]() 和直线
和直线![]() :
:![]() ,射线
,射线![]() 的一个法向量为
的一个法向量为![]() ,点
,点![]() 为坐标原点,且
为坐标原点,且![]() ,直线
,直线![]() 和
和![]() 之间的距离为2,点
之间的距离为2,点![]() ,
,![]() 分别是直线
分别是直线![]() 和
和![]() 上的动点,
上的动点,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,
,![]() ,且
,且![]() ,试求
,试求![]() 的最小值;
的最小值;
(3)若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次体育兴趣小组的聚会中,要安排6人的座位,使他们在如图所示的6个椅子中就坐,且相邻座位(如1与2,2与3)上的人要有共同的体育兴趣爱好.现已知这6人的体育兴趣爱好如下表所示,且小林坐在1号位置上,则4号位置上坐的是
小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |

A.小方B.小张C.小周D.小马
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,公比q>0,S2=2a2-2,S3=a4-2,数列{an}满足a2=4b1,nbn+1-(n+1)bn=n2+n,(n∈N*).
(1)求数列{an}的通项公式;
(2)证明数列{![]() }为等差数列;
}为等差数列;
(3)设数列{cn}的通项公式为:Cn= ,其前n项和为Tn,求T2n.
,其前n项和为Tn,求T2n.
查看答案和解析>>
科目:高中数学 来源: 题型:
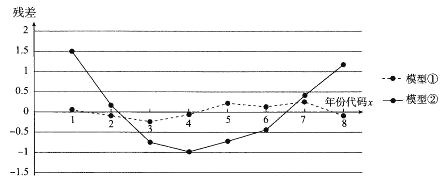
【题目】光伏发电是利用太阳能电池及相关设备将太阳光能直接转化为电能.近几年在国内出台的光伏发电补贴政策的引导下,某地光伏发电装机量急剧上涨,如下表:

某位同学分别用两种模型:①![]() ②
②![]() 进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于
进行拟合,得到相应的回归方程并进行残差分析,残差图如下(注:残差等于![]() ):
):
经过计算得![]() ,
,![]() .
.
(1)根据残差图,比较模型①,②的拟合效果,应该选择哪个模型?并简要说明理由.
(2)根据(1)的判断结果及表中数据建立y关于x的回归方程,并预测该地区2020年新增光伏装机量是多少.(在计算回归系数时精确到0.01)
附:归直线的斜率和截距的最小二乘估计公式分别为: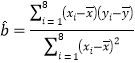 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,
上,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率与直线
的斜率与直线![]() 的斜率乘积为
的斜率乘积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)不经过点![]() 的直线
的直线![]() (
(![]() 且
且![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于原点的对称点为
关于原点的对称点为![]() (与点
(与点![]() 不重合),直线
不重合),直线![]() ,
,![]() 与
与![]() 轴分别交于两点
轴分别交于两点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com