
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 复数z1=2ei${\;}^{\frac{π}{3}}$=2$(cos\frac{π}{3}+isin\frac{π}{3})$=1+$\sqrt{3}$i,z2=ei${\;}^{\frac{π}{2}}$=$cos\frac{π}{2}+isin\frac{π}{2}$=i,再利用复数的运算法则、几何意义即可得出.
解答 解:复数z1=2ei${\;}^{\frac{π}{3}}$=2$(cos\frac{π}{3}+isin\frac{π}{3})$=1+$\sqrt{3}$i,z2=ei${\;}^{\frac{π}{2}}$=$cos\frac{π}{2}+isin\frac{π}{2}$=i,
则复数z=$\frac{{z}_{1}}{{z}_{2}}$=$\frac{1+\sqrt{3}i}{i}$=$\frac{-i(1+\sqrt{3}i)}{-ii}$=$\sqrt{3}$-i在复平面内对应的点$(\sqrt{3},-1)$在第四象限.
故选:D.
点评 本题考查了复数的指数与三角函数形式、复数的运算法则几何意义,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{5}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24里 | B. | 48里 | C. | 96里 | D. | 192里 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{5}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
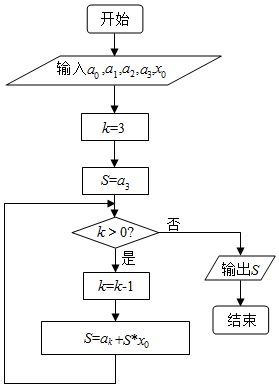
| A. | a0+a1+a2+a3的值 | B. | a3+a2x0+a1x02+a0x03的值 | ||
| C. | a0+a1x0+a2x02+a3x03的值 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 6 | C. | 7 | D. | $\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com