
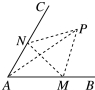
 如图所示,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:千米).
如图所示,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:千米).分析 (1)在△AMN中,利用正弦定理求得△AMN的外接圆的半径R,可得△AMN的外接圆的面积.
(2)设∠AMN=θ,0°<θ<120°,可得AN、∠ANP的值,再利用余弦定理求得AP2的解析式,利用正弦函数的最值,求得AP的最大值.
解答 解:(1)在△AMN中,由正弦定理可知:$\frac{2}{sin60°}$=2R,故△AMN的外接圆的半径 R=$\frac{2\sqrt{3}}{3}$,
∴△AMN的外接圆的面积S=πR2=$\frac{4π}{3}$.
(2)设∠AMN=θ,0°<θ<120°,在△AMN中,$\frac{AN}{sinθ}$=$\frac{2}{sin60°}$,AN=$\frac{4}{\sqrt{3}}$sinθ,
又因为NP=2,∠ANP=180°-θ,∴AP2=AN2+NP2-2AN•NP•cos(180°-θ)=$\frac{16}{3}$sin2θ+4+2•$\frac{4}{\sqrt{3}}$sinθ•2cosθ=$\frac{16}{3}$sin(2θ-30°)+$\frac{20}{3}$.
∵0°<θ<120°,∴-30°<2θ-30°<210°,故当2θ-30°=90°时,AP2取得最大值为$\frac{16}{3}$+$\frac{20}{3}$=12,
故AP的最大值为2$\sqrt{3}$,此时,AM=AN=2.
点评 本题主要考查整弦定理、余弦定理的应用,正弦函数的最值,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | {5,6} | B. | {3,4,5,6} | C. | {1,2,5,6} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{11}}}{4}$ | D. | $\frac{{\sqrt{15}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | af(a)<bf(b) | B. | af(b)<bf(a) | C. | af(a)>bf(b) | D. | af(b)>bf(a) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com