
分析 由平面图形的性质向空间物体的性质进行类比时,常用的思路有:由平面图形中点的性质类比推理出空间里的线的性质,由平面图形中线的性质类比推理出空间中面的性质,由平面图形中面的性质类比推理出空间中体的性质.故我们可以根据已知中平面几何中,关于线的性质“正三角形内任意一点到三边距离之和是一个定值”,推断出一个空间几何中一个关于面的性质.
解答 解:类比在边长为a的正三角形内任一点到三边的距离之和为定值$\frac{{\sqrt{3}}}{2}a$,
在一个正四面体中,计算一下棱长为a的三棱锥内任一点到各个面的距离之和,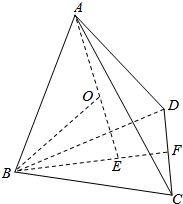
如图:
由棱长为a可以得到BF=$\frac{{\sqrt{3}}}{2}a$,BO=AO=$\frac{\sqrt{6}}{3}$a-OE,
在直角三角形中,根据勾股定理可以得到
BO2=BE2+OE2,
把数据代入得到OE=$\frac{\sqrt{6}}{12}$a,
∴棱长为a的三棱锥内任一点到各个面的距离之和4×$\frac{\sqrt{6}}{12}$a=$\frac{{\sqrt{6}}}{3}a$.
故答案为:$\frac{{\sqrt{6}}}{3}a$.
点评 本题是基础题,考查类比推理及正四面体的体积的计算,转化思想的应用,考查空间想象能力,计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
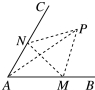 如图所示,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:千米).
如图所示,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:千米).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-13)∪(-13,0) | B. | (-∞,0) | C. | (-13,0) | D. | (-13,0)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
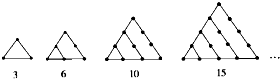 把3、6、10、15、21、…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图),试求第六个三角形数是( )
把3、6、10、15、21、…这些数叫做三角形数,这是因为这些数目的点子可以排成一个正三角形(如图),试求第六个三角形数是( )| A. | 27 | B. | 28 | C. | 29 | D. | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com