
分析 由题意可知,f(x)=(1-2x)10是一个复合函数.是由f(x)=u10,u=1-2x复合而成的.
f′(x)其实是一个复合函数的导数,再利用二项式系数的性质即可解决问题.
解答 解:∵f(x)=(1-2x)10是一个复合函数.
∴f′(x)=10(1-2x)9×(1-2x)′,
f′(x)=-20(1-2x)9,
∵二项展开式-20×(1-2x)9的通项公式为Tr+1=$-20×{C}_{9}^{r}(-2x)^{r}$,
要得到x2项,∴r=2,
所以x2项的系数为-20${×C}_{9}^{2}×(-2)^{2}$=-2880,
故答案为-:-2880.
点评 本题考查了复合函数求导的计算,二项式系数的性质,二项式展开式的通项公式,体现了转化的数学思想,属于基础题.


科目:高中数学 来源: 题型:解答题
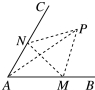 如图所示,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:千米).
如图所示,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M,N(异于村庄A),要求PM=PN=MN=2(单位:千米).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-13)∪(-13,0) | B. | (-∞,0) | C. | (-13,0) | D. | (-13,0)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
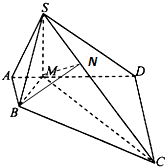 如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD.
如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com