
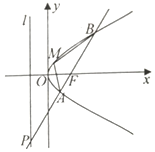
 如图,F为抛物线y2=2px(p>0)的焦点,经过F点作倾斜角为锐角的直线l,与准线及抛物线的交点自下至上依次为P,A,B,且$\overrightarrow{PA}$=2$\overrightarrow{AF}$.
如图,F为抛物线y2=2px(p>0)的焦点,经过F点作倾斜角为锐角的直线l,与准线及抛物线的交点自下至上依次为P,A,B,且$\overrightarrow{PA}$=2$\overrightarrow{AF}$.分析 (Ⅰ)由抛物线的定义,结合题意求出直线l的倾斜角和斜率;
(Ⅱ)写出直线l的方程,与抛物线方程联立消去y,得关于x的方程,利用抛物线的定义求出AB,再求出M到直线l的距离d,计算△MAB的面积最大值,从而求出p的值.
解答 解:(Ⅰ)如图所示,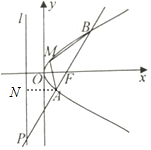
过A作AN垂直准线l,垂足为N,
由抛物线的定义可得AF=AN,
∵$\overrightarrow{PA}$=2$\overrightarrow{AF}$.∴PA=2AN,
∴∠PAN=60°,
∴直线l的斜率为tan60°=$\sqrt{3}$;
(Ⅱ)由(Ⅰ)得直线l的方程为y=$\sqrt{3}$(x-$\frac{p}{2}$),与抛物线方程联立,
得$\left\{\begin{array}{l}{y=\sqrt{3}(x-\frac{p}{2})}\\{{y}^{2}=2px}\end{array}\right.$,消去y,得3x2-5px+$\frac{{3p}^{2}}{4}$=0,
∴x1+x2=$\frac{5p}{3}$,
∴AB=AF+BF=x1+x2+p=$\frac{8p}{3}$;
设M($\frac{{{y}_{0}}^{2}}{2p}$,y0),直线l:$\sqrt{3}$x-y-$\frac{\sqrt{3}}{2}$p=0,
则M到直线l的距离为
d=$\frac{|\frac{{{\sqrt{3}y}_{0}}^{2}}{2p}{-y}_{0}-\frac{\sqrt{3}}{2}p|}{\sqrt{3+1}}$=$\frac{1}{2}$×|$\frac{\sqrt{3}}{2p}$${{y}_{0}}^{2}$-y0-$\frac{\sqrt{3}}{2}$p|,
△MAB的面积为
S△MAB=$\frac{1}{2}$×$\frac{8p}{3}$×$\frac{1}{2}$×|$\frac{\sqrt{3}}{2p}$${{y}_{0}}^{2}$-y0-$\frac{\sqrt{3}}{2}$p|
=$\frac{1}{3}$×|$\sqrt{3}$${{y}_{0}}^{2}$-2py0-$\sqrt{3}$p2|
=$\frac{1}{3}$×|$\sqrt{3}$${{(y}_{0}-\frac{1}{\sqrt{3}}p)}^{2}$-$\frac{4\sqrt{3}}{3}$p2|,
当y0=$\frac{1}{\sqrt{3}}$p时,△MAB取得最大值为$\frac{4\sqrt{3}}{9}$p2=$\sqrt{3}$,
解得p=$\frac{3}{2}$.
点评 本题考查了抛物线的定义与应用问题,也考查了三角形面积的计算问题,是综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x≠0且y≠0 | B. | x=0且y≠0 | C. | x≠0或y≠0 | D. | x=0或y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,面积为S的平面凸四边形的第i条边的边长记为ai(i=1,2,3,4),此四边形内任一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{2}=\frac{a_3}{3}=\frac{a_4}{4}$=k,则h1+2h2+3h3+4h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{2}=\frac{S_3}{3}=\frac{S_4}{4}$=K,则H1+2H2+3H3+4H4等于( )
如图所示,面积为S的平面凸四边形的第i条边的边长记为ai(i=1,2,3,4),此四边形内任一点P到第i条边的距离记为hi(i=1,2,3,4),若$\frac{a_1}{1}=\frac{a_2}{2}=\frac{a_3}{3}=\frac{a_4}{4}$=k,则h1+2h2+3h3+4h4=$\frac{2S}{k}$.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若$\frac{S_1}{1}=\frac{S_2}{2}=\frac{S_3}{3}=\frac{S_4}{4}$=K,则H1+2H2+3H3+4H4等于( )| A. | $\frac{V}{2K}$ | B. | $\frac{2V}{K}$ | C. | $\frac{V}{3K}$ | D. | $\frac{3V}{K}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com