
分析 (1)线段AB的中点E$(\frac{3}{2},\frac{5}{2})$,kAB=-1,可得线段AB的中垂线方程.因为圆C经过A,B两点,故圆心在线段AB的中垂线上.又因为直线m:3x-2y=0平分圆C,所以直线m经过圆心.联立解得圆心C的坐标,利用两点之间距离公式可得圆的半径r,即可得出圆的方程.
(2)设M(x1,y1),N(x2,y2),将y=kx+2代入方程圆的方程,可得(1+k2)x2-(2k+4)x+4=0,△>0,得k的取值范围,利用根与系数的关系可得$\overrightarrow{OM}$•$\overrightarrow{ON}$,代入$\overrightarrow{OM}$•$\overrightarrow{ON}$=6.解出k即可判断出结论.
解答 解:(1)线段AB的中点E$(\frac{3}{2},\frac{5}{2})$,kAB=$\frac{3-2}{1-2}$=-1,
故线段AB的中垂线方程为y-$\frac{5}{2}$=$x-\frac{3}{2}$,即x-y+1=0.…(1分)
因为圆C经过A,B两点,故圆心在线段AB的中垂线上.
又因为直线m:3x-2y=0平分圆C,所以直线m经过圆心.
由$\left\{\begin{array}{l}{x-y+1=0}\\{3x-2y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,
即圆心的坐标为C(2,3),…(3分)
而圆的半径r=|BC|=$\sqrt{(2-2)^{2}+(2-3)^{2}}$=1,…(4分)
所以圆C的方程为:(x-2)2+(y-3)2=1.…(5分)
(2)设M(x1,y1),N(x2,y2),
将y=kx+2代入方程圆的方程,即(1+k2)x2-(2k+4)x+4=0,(*).
由△=(2k+4)2-16(1+k2)>0,得$0<k<\frac{4}{3}$,
∴x1+x2=$\frac{2k+4}{1+{k}^{2}}$,x1x2=$\frac{4}{1+{k}^{2}}$,…(7分)
∴$\overrightarrow{OM}$•$\overrightarrow{ON}$=x1x2+y1y2=x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+2k(x1+x2)+4=6,
∴(1+k2)$\frac{4}{1+{k}^{2}}$+2k$•\frac{2k+4}{1+{k}^{2}}$+4=6,
即3k2+4k+1=0,
解得k=-1,或k=-$\frac{1}{3}$.…(10分)
此时不满足△>0,与直线l与C于M,N两点相矛盾,
所以不存在直线l,使得$\overrightarrow{OM}$•$\overrightarrow{ON}$=6.…(12分)
点评 本题考查了直线与圆相交关系、一元二次方程的根与系数的关系、向量数量积运算性质、中垂线的应用,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{17}$ | C. | 17 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
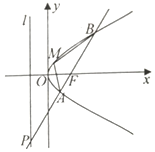 如图,F为抛物线y2=2px(p>0)的焦点,经过F点作倾斜角为锐角的直线l,与准线及抛物线的交点自下至上依次为P,A,B,且$\overrightarrow{PA}$=2$\overrightarrow{AF}$.
如图,F为抛物线y2=2px(p>0)的焦点,经过F点作倾斜角为锐角的直线l,与准线及抛物线的交点自下至上依次为P,A,B,且$\overrightarrow{PA}$=2$\overrightarrow{AF}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com