Question

16．已知△ABC中，AB=AC=4，BC=4$\sqrt{3}$，已知蚂蚁在△ABC的内部爬行，若不考虑蚂蚁的大小，则某时刻该蚂蚁距离△ABC的三个顶点距离均超过1的概率为1-$\frac{\sqrt{3}π}{24}$．

Answer 1

分析 分别求出对应事件所表示的面积，利用几何概型的概率公式计算即可．

解答 解：∵三角形的三边长分别是4，4，4$\sqrt{3}$，
∴三角形的高AD=2，
则△ABC的面积为S=$\frac{1}{2}$×4$\sqrt{3}$×2=4$\sqrt{3}$；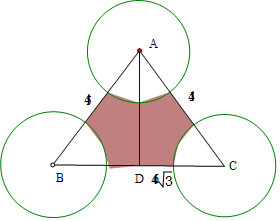

则该蚂蚁距离三角形的三个顶点的距离均超过1，对应的区域为图中阴影部分，
三个小扇形的面积之和为一个整圆的面积的$\frac{1}{2}$，圆的半径为1，
则阴影部分的面积为S₁=4$\sqrt{3}$-$\frac{1}{2}$π•1²=4$\sqrt{3}$-$\frac{1}{2}$π，
根据几何概型的概率公式得所求概率为
P=$\frac{4\sqrt{3}-\frac{1}{2}π}{4\sqrt{3}}$=1-$\frac{\sqrt{3}π}{24}$．
故答案为：1-$\frac{\sqrt{3}π}{24}$．

点评 本题考查了几何概型的概率计算问题，是中档题．