
分析 (1)设|AF1|=x,|AF2|=y,利用椭圆的定义,四边形AF1BF2为矩形,可求出x,y的值,进而可得双曲线的几何量,即可求出双曲线的标准方程;
(2)S${\;}_{△{F}_{1}A{F}_{2}}$=$\frac{1}{2}xy$,即可得出结论.
解答 解:(1)设|AF1|=x,|AF2|=y,
∵点A为椭圆C1:$\frac{{x}^{2}}{4}$+y2=1上的点,
∴2a=4,b=1,c=$\sqrt{3}$;
∴|AF1|+|AF2|=2a=4,即x+y=4;①
又四边形AF1BF2为矩形,∴x2+y2=(2c)2=12,②
由①②解得x=2-$\sqrt{2}$,y=2+$\sqrt{2}$
设双曲线C2的实轴长为2a′,焦距为2c′,
则2a′=|AF2|-|AF1|=y-x=2$\sqrt{2}$,2c′=2$\sqrt{3}$,∴b=1…(5分)
∴双曲线C2的标准方程为$\frac{{x}^{2}}{2}-{y}^{2}$=1; …(8分)
(2)由(1)可得S${\;}_{△{F}_{1}A{F}_{2}}$=$\frac{1}{2}xy$=1.…(12分)
点评 本题考查椭圆与双曲线的简单性质,考查三角形面积的计算,求得|AF1|与|AF2|是关键,考查分析与运算能力,属于中档题.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 7 | 9 | 10 | 11 | 13 |
| y | 40 | 75 | 70 | 90 | 105 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
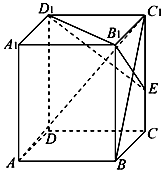 在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.
在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1交CC1于点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | log23 | B. | 8 | C. | log23或8 | D. | 8或6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-i | B. | 1-i | C. | -1+i | D. | 1+i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com