
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 多4个命题分别进行判断,即可得出结论.
解答 解:①命题p:任意x∈R,都有cosx≤1,则“非p”:存在x0∈R,使得cosx0>1,故不正确.
②命题“若a>2且b>2,则a+b>4且ab>4”的逆命题为“若a+b>4且ab>4,则a>2且b>2”是假命题,故否命题为假命题,正确.
③空间任意一点O和不共线的三点A、B、C,若$\overrightarrow{OP}$=2$\overrightarrow{OA}$-$\overrightarrow{OB}$+$\overrightarrow{OC}$,∵2-1+1≠1,∴P、A、B、C四点不共面,不正确.
④线性回归方程y=bx+a对应的直线一定经过其样本中心点,不正确.
故选C.
点评 本题考查命题的真假判断与运用,考查学生分析解决问题的能力,涉及知识点多.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
 如图,网格纸上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为
如图,网格纸上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为| A. | 9π | B. | 18π | C. | 36π | D. | 144π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
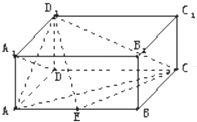 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
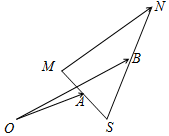 如图,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,任意点M关于点A的对称点为S,点S关于点B的对称点为N,则向量$\overrightarrow{MN}$=2$\overrightarrow{b}$-2$\overrightarrow{a}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{MN}$)
如图,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,任意点M关于点A的对称点为S,点S关于点B的对称点为N,则向量$\overrightarrow{MN}$=2$\overrightarrow{b}$-2$\overrightarrow{a}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{MN}$)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com