
 如图,网格纸上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为
如图,网格纸上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为| A. | 9π | B. | 18π | C. | 36π | D. | 144π |
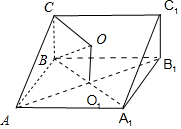
分析 由三视图可知:该几何体为一个横放的直三棱柱,高为4,底面是一个直角边长分别为2,4的直角三角形,其中下面的一个侧面为边长为4的正方形,对角线相交于点O1.则球心O满足OO1⊥侧面ABB1A1.设OO1=x,则x2+$(2\sqrt{2})^{2}$=(2-x)2+$(2\sqrt{2})^{2}$,解得x.可得该多面体外接球的半径r.
解答 解:由三视图可知:该几何体为一个横放的直三棱柱,高为4,底面是一个直角边长分别为2,4的直角三角形,其中下面的一个侧面为边长为4的正方形,对角线相交于点O1.
则球心O满足OO1⊥侧面ABB1A1.
设OO1=x,则x2+$(2\sqrt{2})^{2}$=(2-x)2+$(2\sqrt{2})^{2}$,解得x=1.
∴ 该多面体外接球的半径r=$\sqrt{{1}^{2}+(2\sqrt{2})^{2}}$=3.
该多面体外接球的半径r=$\sqrt{{1}^{2}+(2\sqrt{2})^{2}}$=3.
表面积为4π×32=36π.
故选:C.
点评 本题考查了直三棱柱的三视图、勾股定理、空间线面位置关系、球的表面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{64}{27}$ | B. | $\frac{{64\sqrt{3}}}{9}$ | C. | $\frac{64}{9}$ | D. | $\frac{{64\sqrt{3}}}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 350里 | B. | 1050里 | C. | $\frac{175}{32}$里 | D. | .$\frac{22575}{32}$里 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com