
分析 根据题意,首先有基本不等式可得1=a+b≥2$\sqrt{ab}$,即$\sqrt{ab}$≤$\frac{1}{2}$,对于a2+b2,将其变形可得a2+b2=(a+b)2-2ab=1-2ab,结合$\sqrt{ab}$≤$\frac{1}{2}$,分析可得其最小值;对于$\sqrt{a}+\sqrt{b}$,有($\sqrt{a}+\sqrt{b}$)2=a+b+2$\sqrt{ab}$=1+2$\sqrt{ab}$,结合$\sqrt{ab}$≤$\frac{1}{2}$,分析可得其最大值;即可得答案.
解答 解:根据题意,若正实数a,b满足a+b=1,则有1=a+b≥2$\sqrt{ab}$,即$\sqrt{ab}$≤$\frac{1}{2}$,
a2+b2=(a+b)2-2ab=1-2ab≥$\frac{1}{2}$,即a2+b2最小值是$\frac{1}{2}$,
对于$\sqrt{a}+\sqrt{b}$,有($\sqrt{a}+\sqrt{b}$)2=a+b+2$\sqrt{ab}$=1+2$\sqrt{ab}$≤2,
则有$\sqrt{a}+\sqrt{b}$≤$\sqrt{2}$;
则$\sqrt{a}+\sqrt{b}$最大值是$\sqrt{2}$;
故答案为:$\frac{1}{2}$,$\sqrt{2}$.
点评 本题考查基本不等式的应用,关键要熟悉基本不等式的形式,并能灵活应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
 如图,网格纸上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为
如图,网格纸上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为| A. | 9π | B. | 18π | C. | 36π | D. | 144π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示,则它的体积是( )
某几何体的三视图如图所示,则它的体积是( )| A. | 8-2π | B. | 4-$\frac{2π}{3}$ | C. | 8-$\frac{2π}{3}$ | D. | 4-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
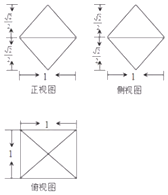
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
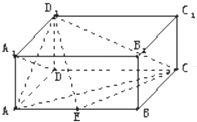 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com